
 如图,线段AB、CD分别表示甲、乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米.
如图,线段AB、CD分别表示甲、乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米.分析 (1)在Rt△ABD中利用三角函数即可求解;
(2)作CE⊥AB于点E,在Rt△BCE中利用三角函数求得BE的长,然后根据CD=AE=AB-BE求解.
解答 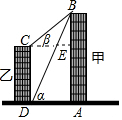 解:(1)作CE⊥AB于点E,
解:(1)作CE⊥AB于点E,
在Rt△ABD中,AD=$\frac{AB}{tanα}$=$\frac{30}{\sqrt{3}}$=10$\sqrt{3}$(米);
(2)在Rt△BCE中,CE=AD=10$\sqrt{3}$米,
BE=CE•tanβ=10$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=10(米),
则CD=AE=AB-BE=30-10=20(米)
答:乙建筑物的高度DC为20m.
点评 本题考查了直角三角形中三角函数的应用,考查了特殊角的三角函数值,本题中求的AD的长是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 平均数是-2 | B. | 中位数是-2 | C. | 众数是-2 | D. | 方差是7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 跳远成绩 | 160 | 170 | 180 | 190 | 200 | 210 |
| 人数 | 3 | 9 | 6 | 9 | 15 | 3 |
| A. | 9,9 | B. | 15,9 | C. | 190,200 | D. | 185,200 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
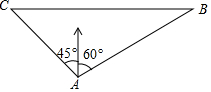 一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为20+20$\sqrt{3}$海里/小时.
一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为20+20$\sqrt{3}$海里/小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com