
【题目】已知抛物线y=(1﹣m)x2﹣mx﹣1与x轴交于A、B两点,顶点为P.
(1)求m的取值范围;
(2)若A、B位于原点两侧,求m的取值范围;
(3)若顶点P在第四象限,求m的取值范围.
【答案】(1)m≠2且m≠1;(2)m<1;(3)0<m<1.
【解析】
(1)根据二次函数与一元二次方程的关系可得△>0,进而可得关于m的不等式,解不等式并结合二次项系数不为0即得结果;
(2)由题意得:y=0时对应方程的两根异号,即x1x2<0,然后根据根与系数的关系解答即可;
(3)先用m的代数式表示出顶点坐标,然后根据顶点的位置可得关于m的不等式组,解不等式组即得结果.
解:(1)根据题意,得:△=m2+4(1﹣m)>0,且1﹣m≠0,解得:m≠2且m≠1;
(2)设A(x1,0)、B(x2,0),则x1、x2是(1﹣m)x2﹣mx﹣1=0的两个根,由题意得:x1x2<0,即![]() ,解得:m<1;
,解得:m<1;
(3)由顶点坐标公式可得:点P的坐标为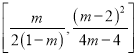 ,
,
∵点P在第四象限,∴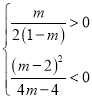 ,解得:0<m<1.
,解得:0<m<1.


科目:初中数学 来源: 题型:
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
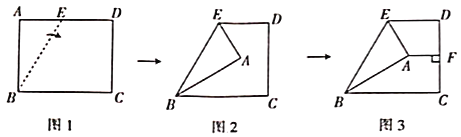
【题目】在学习了矩形后,数学活动小组开展了探究活动.如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,先以
上,先以![]() 为折痕将
为折痕将![]() 点往右折,如图2所示,再过点
点往右折,如图2所示,再过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示.
,如图3所示.
(1)在图3中,若![]() ,则
,则![]() 的度数为______,
的度数为______,![]() 的长度为______.
的长度为______.
(2)在(1)的条件下,求![]() 的长.
的长.
(3)在图3中,若![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图矩形![]() 是矩形ABCD的“减半”矩形.
是矩形ABCD的“减半”矩形.
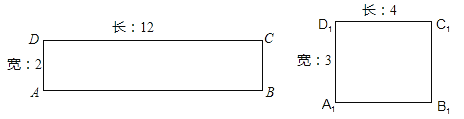
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
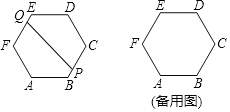
【题目】一个边长为60米的正六边形跑道,P、Q两人同时从A处开始沿相反方向都跑一圈后停止,P以4米/秒逆时针方向、Q以5米/秒顺时针方向,PQ的距离为d米,设跑步时间为x秒,令d2=y,
(1)跑道全长为 米,经过 秒两人第一次相遇.
(2)当P在BC上,Q在EF上时,求y关于x的函数解析式;并求相遇前当x为多少时,他们之间的距离最大.
(3)直接写出P、Q在整个运动过程中距离最大时的x的值及最大的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是y=x2﹣(k+2)x+2k﹣2.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若抛物线与直线y=x+k2﹣1的一个交点在y轴上,求该二次函数的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
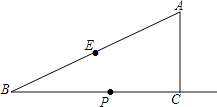
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com