
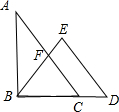
 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,∠D=48°,∠ABE=42°,请求出∠ACB的度数.
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,∠D=48°,∠ABE=42°,请求出∠ACB的度数. 分析 首先证明△ABC≌△DEB,推出∠A=∠D=48°,∠ACB=∠DBE,由∠ABE=42°,推出∠FBC=∠A+∠ABE=90°,推出∠FBC=∠FCB=45°即可解决问题.
解答 解:在△ ABC和△DEB中,
ABC和△DEB中,
$\left\{\begin{array}{l}{AB=DE}\\{AC=BD}\\{BC=BE}\end{array}\right.$,
∴△ABC≌△DEB,
∴∠A=∠D=48°,∠ACB=∠DBE,
∵∠ABE=42°,
∴∠FBC=∠A+∠ABE=90°,
∴∠FBC=∠FCB=45°,
即∠ACB=45°.
点评 本题考查全等三角形平的判定和性质、三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于基础题中考常考题型.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
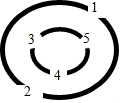 如图,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.
如图,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
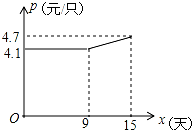 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系式:y=$\left\{\begin{array}{l}{50x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系式:y=$\left\{\begin{array}{l}{50x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
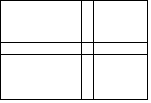 如图,为美化校园环境,学校计划在一块肠胃22米,宽为17米的矩形地面上修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一边平行),剩余部分种上花草,并使花草种植面积为300平方米.请问道路宽度为多少米?
如图,为美化校园环境,学校计划在一块肠胃22米,宽为17米的矩形地面上修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一边平行),剩余部分种上花草,并使花草种植面积为300平方米.请问道路宽度为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com