
分析 (1)利用直接开平方法解方程即可;
(2)先由根与系数的关系得出x1+x2=$\sqrt{6}$,x1x2=-$\sqrt{2}$,再将$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$变形为两根之积或两根之和的形式,代入数值计算即可.
解答 解:(1)(3x-2)2=(2x-3)2,
3x-2=2x-3或3x-2=-2x+3,
解得:x1=-1,x2=1;
(2)由根与系数的关系得:x1+x2=$\sqrt{6}$,x1x2=-$\sqrt{2}$,
所以,$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{\sqrt{6}}{-\sqrt{2}}$=-$\sqrt{3}$.
故答案为-$\sqrt{3}$
点评 此题考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.也考查了利用直接开平方法解方程.


科目:初中数学 来源: 题型:解答题
 如图,在面积为48a2cm2(a>0)的正方形的四角处,分别剪去四个面积均为3cm2的小正方形,制成一个无盖的长方体盒子.
如图,在面积为48a2cm2(a>0)的正方形的四角处,分别剪去四个面积均为3cm2的小正方形,制成一个无盖的长方体盒子.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC$\frac{1}{2}$∠BAC.其中正确的结论( )
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC$\frac{1}{2}$∠BAC.其中正确的结论( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
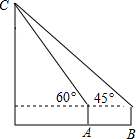 小宇想测量他所就读学校的高度,他先站在点A处,仰视旗杆的顶端C,此时他的视线的仰角为60°,他再站在点B处,仰视旗杆的顶端C,此时他的视线的仰角为45°,如图所示,若小宇的身高为1.5m,旗杆的高度为10.5cm,则AB的距离为( )
小宇想测量他所就读学校的高度,他先站在点A处,仰视旗杆的顶端C,此时他的视线的仰角为60°,他再站在点B处,仰视旗杆的顶端C,此时他的视线的仰角为45°,如图所示,若小宇的身高为1.5m,旗杆的高度为10.5cm,则AB的距离为( )| A. | 9m | B. | (9-$\sqrt{3}$)m | C. | (9-3$\sqrt{3}$)m | D. | 3$\sqrt{3}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com