
分析 方法(1):可将不等式化为3x-6<0,作出直线y=3x-6,然后观察:自变量x取何值时,图象上的点在x轴下方.
方法(2):画出直线y=6x-4与y=3x+2,然后观察:对于哪些x的值,直线y=6x-4上的点在直线y=3x+2上相应的点的下方.
解答 解:方法(1):
原不等式化为3x-6<0,在直角坐标系中画出函数y=3x-6的图象(图1).从图象可以看出,当x<2时这条直线上的点在x轴下方,即这时y=3x-6<0,因此不等式的解集是x<2.
方法(2):
在同一坐标系中画出直线y=6x-4与y=3x+2(图2),从图象上可以看出它们的交点的横坐标是x=2,因此当x<2时,对于同一个x的值,直线y=6x-4上的点在直线y=3x+2上相应的点的下方,此时有6x-4<3x+2,因此不等式的解集是x<2.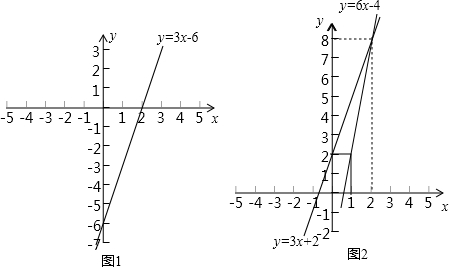
点评 本题考查了一次函数与一元一次不等式,属于基础题,关键是用数形结合的思想解题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
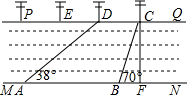 如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
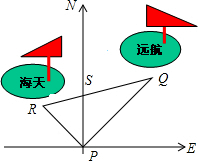 如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile
如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一张长为5,宽为1的矩形纸片,要通过适当的剪拼,得到一个与之面积相等的正方形
如图,有一张长为5,宽为1的矩形纸片,要通过适当的剪拼,得到一个与之面积相等的正方形查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com