
����Ŀ��ijУΪ�˽�ȫУ2000��ѧ���Ŀ����Ķ��������ȫУ��Χ�����������50��ѧ�����õ�������ijһ����Կ����Ķ�����ʱ������ݣ���������Ƴ�Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ���� 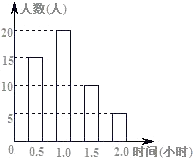
��1����50��ѧ������һ������Ķ�����ʱ��������Ƕ��٣�
��2����50��ѧ������һ��ƽ��ÿ�˵Ŀ����Ķ�����ʱ���Ƕ��٣�
��3������������ϵ��飬����ȫУѧ��������һ������Ķ�����ʱ����1.0Сʱ���ϣ���1.0Сʱ�����ж����ˣ�
���𰸡�
��1���⣺������1.0��Сʱ��
��2���⣺x= ![]() ��0.5��15+1.0��20+1.5��10+2.0��5��=1.05��Сʱ����
��0.5��15+1.0��20+1.5��10+2.0��5��=1.05��Сʱ����
��50��ѧ������һ��ƽ��ÿ�˵Ŀ����Ķ�����ʱ����1.05Сʱ
��3���⣺2000�� ![]() =1400��
=1400��
����ȫУѧ��������һ������Ķ�����ʱ����1.0Сʱ���ϣ���1.0Сʱ����ԼΪ1400��
����������1�����������ĸ�����ִ����������ݣ���1.0���ֵĴ�����࣬��20�Σ�����������1.0����2�����ݼ�Ȩƽ����������ȷ���㣻��3�����ȼ�����������һ������Ķ�����ʱ����1.0Сʱ���ϵ�Ƶ�ʣ��ٽ�һ������ȫУѧ��������һ������Ķ�����ʱ����1.0Сʱ���ϵ�������
�����㾫��������Ƶ���ֲ�ֱ��ͼ������ƽ��������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������������ܷ���=ƽ����������ؼ��Ǹ�����֪����ȷ���������Լ��������Ӧ���ܷ�����


 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD����࣬���ȱߡ�ADE��AC��BE�ཻ�ڵ�F�����EFCΪ�� �� 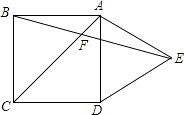
A.135��
B.145��
C.120��
D.165��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2��x��1��x���һ�����������Ϊ(m��0)�������ʽm2��m��2019��ֵΪ(�� ��)
A. 2015B. 2016C. 2019D. 2020
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1����15������8��+����11����12
��2����23+[����4��2����1��32����3]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x��1�뷴��������y= ![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m����
��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m���� 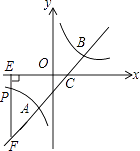
��1�������������Ľ���ʽΪ �� ֱ��y=x��1��˫����y= ![]() �Ϸ�ʱx��ȡֵ��Χ����
�Ϸ�ʱx��ȡֵ��Χ����
��2������P��n����1���Ƿ���������ͼ����һ�㣬����P��PE��x���ڵ�E���ӳ�EP��ֱ��AB�ڵ�F�����CEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ܳ�Ϊ80cm�������Σ����ĸ��Ǹ���ȥһ�������Σ�����һ���Ǻ��ӡ���������ӵĵ������Ϊy cm����ȥ�������εı߳�Ϊx cm����y��x�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=��x����k+1����˫����y= ![]() �ཻ��B��C���㣬��x���ཻ��A�㣬BM��x�ύx���ڵ�M��S��OMB=
�ཻ��B��C���㣬��x���ཻ��A�㣬BM��x�ύx���ڵ�M��S��OMB= ![]()
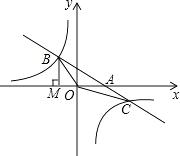
��1���������������Ľ���ʽ��
��2������֪��C�ĺ�����Ϊ3����A��C�������ꣻ
��3���ڣ�2�������£��Ƿ���ڵ�P��ʹ��A��O��C��PΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ����ȷ���ǣ� ��
A.�� ![]() ��
�� ![]() ����x��y
����x��y
B.��bx��by����x��y
C.�� ![]() =
= ![]() ����x=y
����x=y
D.��mx=my����x=y
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com