
【题目】(2019·济源一模)为支持国家南水北调工程建设,小王家由原来养殖户变为种植户, 经市场调查得知,种植草莓不超过20亩时,所得利润 y(元)与种植面积 m(亩)满足关系式y=1500 m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系式为z=-20x+2 100.
(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量的取值范围;
(2)如果小王家计划承包40亩荒山种植草莓和樱桃,当种植樱桃面积(x亩)满足0<x<20时,求小王家总共获得的利润w(元)的最大值.
【答案】(1)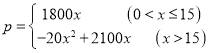 ;(2)①当x=15时,w最大,最大值为63900;②当x=18时,小王家总共获得的利润w取最大值,最大值为64080元.
;(2)①当x=15时,w最大,最大值为63900;②当x=18时,小王家总共获得的利润w取最大值,最大值为64080元.
【解析】
(1)根据图表的性质,可以得出P关于x的函数关系式和出x的取值范围.
(2)根据利润=亩数×每亩利润,可得①当0<x≤15时 ②当15<x<20时,利润的函数式,即可解题;
解:(1)由题意得:
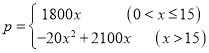
(2)种植樱桃面积x亩,则种植草莓面积(40-x)亩,
由题意知,
①当0<x≤15时,w=1800x+1380(40-x)+2400
=420x+57600,
∵420>0,
∴w随x的增大而增大,
当x=15时,w最大,最大值为63900,
②当15<x≤20时,w=-20x2+2100x+1380(40-x)+2400
=-20(x-18)2+64080,
∵-20<0,
∴当x=18时,w取最大值,最大值为64080,
∵64080>63900,
∴当x=18时,小王家总共获得的利润w取最大值,最大值为64080元.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴、y轴上,OA=4,OC=3,直线m:y=﹣![]() x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )
x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )

A. 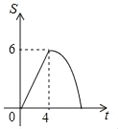 B.
B. 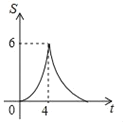 C.
C. 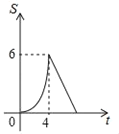 D.
D. 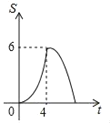
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
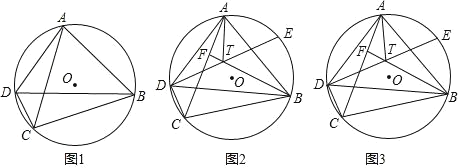
(1)如图1,求证:AC=BC;
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
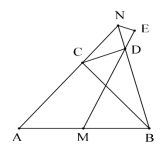
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为 1 的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在 x 轴上、斜边长分别为 2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2019的横坐标为( )
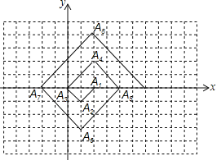
A.-1008B.2C.1D.1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正三角形的一边平行于![]() 轴,一顶点在
轴,一顶点在![]() 轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用
轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用![]() 表示,其中
表示,其中![]() 与
与![]() 轴、底边
轴、底边![]() 与
与![]() 与
与![]() 、…均相距一个单位,则顶点
、…均相距一个单位,则顶点![]() 的坐标是__________,
的坐标是__________,![]() 的坐标是__________.
的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆,半圆恰好经过△ABC的直角顶点C,以点D为顶点,作∠EDF=90°,与半圆交于点E、F,则图中阴影部分的面积是_______.
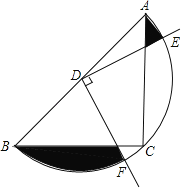
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接AD、CD、OC.填空
①当∠OAC的度数为 时,四边形AOCD为菱形;
②当OA=AE=2时,四边形ACDE的面积为 .
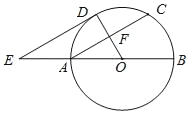
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com