
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.| 组别 | 消费额(元) |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 20≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
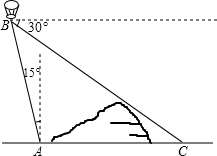 如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)
如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-{2^2}}$ | B. | $\root{3}{{-{2^2}}}$ | C. | $\sqrt{{{(-2)}^2}}$ | D. | $\root{3}{{{{(-2)}^2}}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
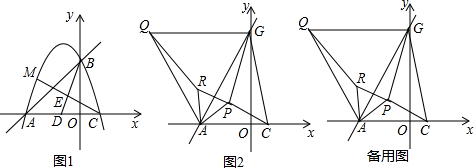
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com