
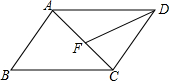
 如图,四边形ABCD是平行四边形,∠BAC=80°,DF是∠CDA的角平分线,交AC于点F,∠CDF=25°,则∠CAD=50°.
如图,四边形ABCD是平行四边形,∠BAC=80°,DF是∠CDA的角平分线,交AC于点F,∠CDF=25°,则∠CAD=50°. 科目:初中数学 来源: 题型:填空题
 如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=74°,则∠NPB′=16°.
如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=74°,则∠NPB′=16°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com