
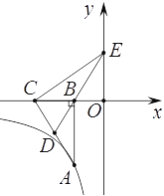
【题目】如图,已知点A在反比例函数![]() 上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8。
上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8。
(1)求证:△EOB∽△ABC;
(2)求反比例函数的解析式。
【答案】(1)证明见解析;(2)16.
【解析】根据反比例函数系数k的几何意义,证明△ABC∽△EOB,根据相似比求出BABO的值,从而求出△AOB的面积.
解:(1)∵在Rt△ABC中,点D为斜边AC的中点,
∴BD=DC,
∴∠DBC=∠DCB=∠EBO,
又∠EOB=∠ABC=90°,
∴△EOB∽△ABC
(2)∵△EOB∽△ABC
∴![]() =
=![]() ,
,
∵△BCE的面积为8,
∴![]() =8,∵
=8,∵![]() =
=![]() ,
,
∴BCOE=16,∴ABOB=BCOE
∴k=ABBO=BCOE=16.
∴反比例函数的解析式为: ![]() .
.
“点睛”本题考查了反比例函数系数k的几何意义,解决本题的关键是证明△EOB∽△ABC,得到ABOB=BCOE,最后求出反比例函数的解析式.


科目:初中数学 来源: 题型:
【题目】小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是( )
A. Q=8x B. Q=8x﹣50 C. Q=50﹣8x D. Q=8x+50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(在矩形ABCD中,AB=4,BC=8,经过对角线交点O的直线EF绕点O旋转,分别交AD、BC于点E、F,连接AF、CE.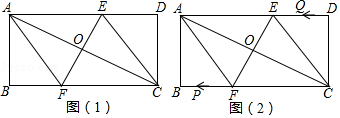
(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空:旋转过程中四边形AFCE始终为;
当点E为AD的中点时四边形AFCE为;
当EF⊥AC时四边形AFCE为;
(2)如图(1),当EF⊥AC时,求AF的长;
(3)如图(2),在(2)的基础上,若动点P从A点出发,沿A→F→B→A运动一周停止,速度为每秒5厘米;同时点Q从C点出发,沿C→D→E→C运动一周停止,速度为每秒4厘米,在P、Q运动过程中,第几秒时,四边形APCQ是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售价格降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国月球探测工程的“嫦娥一号”发射升空飞向月球,已知地球距离月球表面约为384 000千米,那么这个距离用科学记数法表示为( )
A.3.84×104 千米
B.3.84×105千米
C.3.84×106千米
D.38.4×104 千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com