
分析 设安置点有a个帐篷,车队有b辆车,根据“若每个帐篷分配1.5吨物资,则余下不足一车物资;若每个帐篷分配1.6吨物资,则尚差2车多的物资”列出关于a、b的不等式组,在所列不等式组中根据不等式的性质消去未知数a,再求出所得的关于b的不等式的解集,在所得的b的取值范围内取整数代回原不等式组求得a的范围,从而得出答案.
解答 解:设安置点有a个帐篷,车队有b辆车,根据题意得:
$\left\{\begin{array}{l}{10(b-1)<1.5a<10b}\\{10(b+2)<1.6a<10(b+3)}\end{array}\right.$,
即$\left\{\begin{array}{l}{100(b-1)<15a<100b}\\{100(b+2)<16a<100(b+3)}\end{array}\right.$,
解不等式组$\left\{\begin{array}{l}{15a<100b}\\{100(b+2)<16a}\end{array}\right.$,即$\left\{\begin{array}{l}{a<\frac{100}{15}b}\\{\frac{100(b+2)}{16}<a}\end{array}\right.$,
可得b>30,
取b=31,代入$\left\{\begin{array}{l}{100(b-1)<15a<100b}\\{100(b+2)<16a<100(b+3)}\end{array}\right.$,得:$\left\{\begin{array}{l}{3000<15a<3100}\\{3300<16a<3400}\end{array}\right.$
解3000<15a<3100得:200<a≤206,
解3300<16a<3400得:207≤a≤212,
无解;
取b=32,代入$\left\{\begin{array}{l}{100(b-1)<15a<100b}\\{100(b+2)<16a<100(b+3)}\end{array}\right.$,得:$\left\{\begin{array}{l}{3100<15a<3200}\\{3400<16a<3500}\end{array}\right.$,
解3100<15a<3200得:207≤a≤213,
解3400<16a<3500得:213≤a≤218,
∴a=213,
答:这个安置点最少有213顶帐篷.
点评 本题主要考查不等式组的应用,理解题意找到题目蕴含的不等关系列出不等式组并灵活求解是解题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
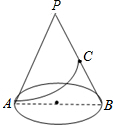 己知底面半径是4cm,母线长为12cm,C为母线PB中点,现在有一只蚂蚁从底边一点A出发.在侧面爬行到C点,则蚂蚁在圆锥侧面爬行最短距离6$\sqrt{3}$cm.
己知底面半径是4cm,母线长为12cm,C为母线PB中点,现在有一只蚂蚁从底边一点A出发.在侧面爬行到C点,则蚂蚁在圆锥侧面爬行最短距离6$\sqrt{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com