
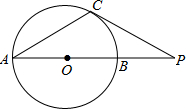
 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线与AB的延长线交于点P.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线与AB的延长线交于点P.分析 (1)只要证明∠PCB+∠OCB=90°,∠A+∠OCB=90°即可解决问题;
(2)只要证明△PCB∽△PAC,可得PC2=PB•PA,求出PA即可解决问题;
(3)由△ACN∽△MCB,可得$\frac{AC}{CM}$=$\frac{AN}{BM}$,求出AC、AN、BM即可解决问题;
解答 解:(1)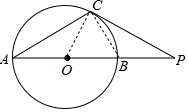 如图,连接OC、BC.
如图,连接OC、BC.
∵PC是切线,
∴PC⊥OC,
∴∠PCB+∠OCB=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠PCB=∠CAP.
(2)∵∠PCB=∠PAC,∠P=∠P,
∴△PCB∽△PAC,
∴$\frac{PC}{PA}$=$\frac{PB}{PC}$,
∴PC2=PB•PA,
∵PB=$\sqrt{3}$,PC=2$\sqrt{6}$,
∴PA=8$\sqrt{3}$,
∴AB=PA-PB=7$\sqrt{3}$,
∴⊙O的半径为$\frac{7}{2}$$\sqrt{3}$.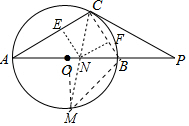
(3)如图,连接OM、BM、作NE⊥AC于E,NF⊥BC于F.
∵△PCB∽△PAC,
∴$\frac{PC}{PA}$=$\frac{CB}{AC}$=$\frac{\sqrt{2}}{4}$,易知AC=$\frac{14}{3}$$\sqrt{6}$,BM=$\frac{7\sqrt{6}}{2}$,
∵CM平分∠ACB,
∴NE=NF,OM⊥AB,
∴∠ACM=∠OBM=45°,
∵$\frac{{S}_{△ACN}}{{S}_{△BCN}}$=$\frac{\frac{1}{2}•AC•NE}{\frac{1}{2}•BC•NF}$=$\frac{AN}{NB}$,
∴AN:BN=AC:BC=4:$\sqrt{2}$,
∴AN=8$\sqrt{3}$-2$\sqrt{6}$,
由△ACN∽△MCB,
∴$\frac{AC}{CM}$=$\frac{AN}{BM}$,
∴$\frac{\frac{14}{3}\sqrt{6}}{CM}$=$\frac{8\sqrt{3}-2\sqrt{6}}{\frac{7\sqrt{6}}{2}}$,
∴CM=$\frac{14\sqrt{3}}{3}$+$\frac{7}{6}$$\sqrt{6}$.
点评 本题考查切线的性质、角平分线的性质、相似三角形的性质和判定等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
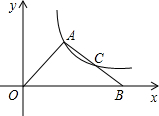 如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )
如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )| A. | 8 | B. | 7.5 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 鞋的尺寸 (单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量 (单位:双) | 1 | 2 | 3 | 4 | 2 |
| A. | 25,25 | B. | 24.5,25 | C. | 24.5,24.5 | D. | 25,24.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.
已知A.B两地相距100km,甲乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶.甲乙两人离A地的距离s(千米)与骑车时间t(小时)满足的函数关系图象如图所示.当甲乙两人相遇时,乙距离A地$\frac{300}{7}$km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com