
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
【答案】
(1)证明:连结OD,

∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
又∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∵OD是⊙O半径,
∴CD是⊙O的切线
(2)解:∵∠C=∠C,∠CDA=∠CBD
∴△CDA∽△CBD
∴ ![]()
∵ ![]() ,BC=6,
,BC=6,
∴CD=4,
∵CE,BE是⊙O的切线
∴BE=DE,BE⊥BC
∴BE2+BC2=EC2,即BE2+62=(4+BE)2
解得:BE= ![]() .
.
【解析】(1)根据直径所对的圆周角是直角,得到∠ADB=90°,由等量代换得到∠CDO=90°,即CD是⊙O的切线;(2)由∠C=∠C,∠CDA=∠CBD,得到△CDA∽△CBD,由比值得到CD=4,由CE,BE是⊙O的切线,得到BE=DE,BE⊥BC,由勾股定理得到BE2+BC2=EC2,求出B![]() E的值.
E的值.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 以
以![]() 的速度从点
的速度从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动.
运动.
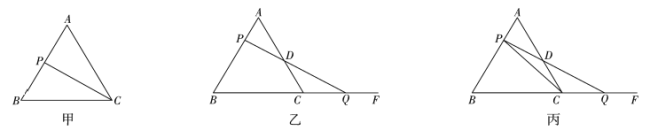
(1)如图甲,设点![]() 的运动时间为
的运动时间为![]() ,那么
,那么![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(2)若另一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,连接
方向运动,连接![]() 交
交![]() 于点
于点![]() ,如果动点
,如果动点![]() 都以
都以![]() 的速度同时出发.
的速度同时出发.
①如图乙,设运动时间为![]() ,那么
,那么![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?
②如图丙,连接![]() ,请你猜想:在点
,请你猜想:在点![]() 的运动过程中,
的运动过程中,![]() 和
和![]() 的面积有什么关系?并说明理由.
的面积有什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )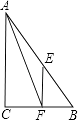
A.△ABC是直角三角形
B.AF是△ABC的中位线
C.EF是△ABC的中位线
D.△BEF的周长为6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①已知直角三角形的面积为4,两直角边的比为1:2,则斜边长为![]() ;②直角三角形的最大边长为
;②直角三角形的最大边长为![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为![]() ;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;④等腰三角形面积为12,底边上的高为4,则腰长为5,其中正确结论的序号是( )
;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;④等腰三角形面积为12,底边上的高为4,则腰长为5,其中正确结论的序号是( )
A. 只有①②③ B. 只有①②④ C. 只有③④ D. 只有②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图.
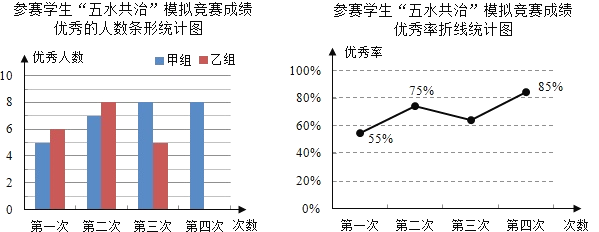
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数![]() ,方差
,方差![]() ,请通过计算说明那一组成绩优秀的人数较稳定?
,请通过计算说明那一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
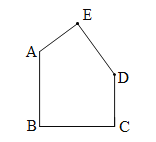
【题目】如图:五边形ABCDE中,AB∥CD,BC⊥AB,AB=BC=8,CD=5.
(1)说明∠A,∠E,∠D之间的数量关系;
(2)平移五边形ABCDE,使D点移动到C点,画出平移后的五边形A'B'C'CE',并求出顺次连接A、A'、E'、C、D、E、A各点所围成的图形的面积;
(3)在∠BAE和∠E'CD的内部取一点F,使∠EAF=![]() ∠EAB,∠FCE'=
∠EAB,∠FCE'=![]() ∠DCE' ,求∠AFC与∠AED之间的数量关系.
∠DCE' ,求∠AFC与∠AED之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com