
【题目】2019年小张前五个月的奖金变化情况如下表(正数表示比前一月多的钱数,负数表示比前一月少的钱数,单位:元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 |
钱数变化 |
|
|
|
|
|
若2018年12月份小张的奖金为![]() 元.
元.
(1)用代数式表示2019年二月份小张的奖金为___________元;
(2)小张五月份所得奖金比二月份多多少?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
①方程![]() 是倍根方程;
是倍根方程;
②若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
③若点![]() 在反比例函数
在反比例函数![]() 的图像上,则关于
的图像上,则关于![]() 的方程
的方程![]() 是倍根方程;
是倍根方程;
④若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() ,
, ![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.
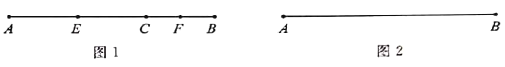
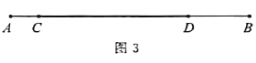
(2)应用:
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《实数》内容时,我们通过“逐步逼近”的方法可以计算出![]() 的近似值,得出1.4<
的近似值,得出1.4<![]() <1.5.利用“逐步逼近“法,请回答下列问题:
<1.5.利用“逐步逼近“法,请回答下列问题:
(1)![]() 介于连续的两个整数a和b之间,且a<b,那么a= ,b= .
介于连续的两个整数a和b之间,且a<b,那么a= ,b= .
(2)x是![]() +2的小数部分,y是
+2的小数部分,y是![]() ﹣1的整数部分,求x= ,y= .
﹣1的整数部分,求x= ,y= .
(3)(![]() ﹣x)y的平方根.
﹣x)y的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,已知在纸面上有一数轴(如图),折叠纸面.
![]()
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与何数表示的点重合;
(2)若﹣1表示的点与5表示的点重合,0表示的点与何数表示的点重合;
(3)若﹣1表示的点与5表示的点之间的线段折叠2次,展开后,请写出所有的折点表示的数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲乙两人在一个200米的环形跑道上练习跑步,现在把跑道分成相等的4段,即两条直道和两条弯道的长度相同.甲平均每秒跑4米,乙平均每秒跑6米,若甲乙两人分别从A、C两处同时相向出发(如图),试解答下列问题:
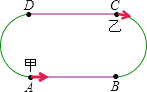
(1)几秒后两人首次相遇?请说出此时他们在跑道上的具体位置;
(2)首次相遇后,又经过多少时间他们再次相遇?
(3)他们第100次相遇时,在哪一段跑道上?(第(3)问直接写出结论即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com