
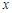 轴交于点C,与双曲线
轴交于点C,与双曲线 交于A(3,
交于A(3,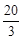 )、B(-5,
)、B(-5, )两点.AD⊥
)两点.AD⊥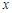 轴于点D,BE∥
轴于点D,BE∥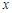 轴且与
轴且与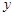 轴交于点E.
轴交于点E.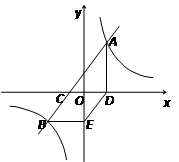
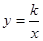 过A(3,
过A(3,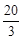 ),∴
),∴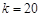 .把B(-5,
.把B(-5, )代入
)代入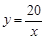 ,
,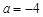 . ∴点B的坐标是(-5,-4).
. ∴点B的坐标是(-5,-4). 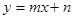 ,
,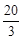 )、B(-5,-4)代入得,
)、B(-5,-4)代入得,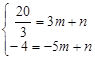 , 解得:
, 解得: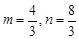 .
. 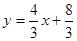 .
. 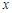 轴, ∴点E的坐标是(0,-4).
轴, ∴点E的坐标是(0,-4). =5,∴ED=CD.
=5,∴ED=CD.

科目:初中数学 来源:不详 题型:解答题
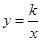 (
( ,
,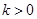 )的图象经过点
)的图象经过点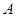 (1,2),
(1,2), (
(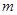 ,
,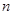 )(
)(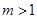 ),过点B作
),过点B作 轴的垂线,垂足为C.
轴的垂线,垂足为C.
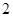 时,求点B的坐标;
时,求点B的坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 、
、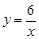 、
、 的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出几条 ( )
的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出几条 ( ) | A.12 | B.13 | C.25 | D.50 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么△AOB的面积为________.
图象在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么△AOB的面积为________.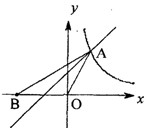
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com