
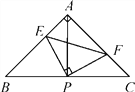
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰三角形;④EF=AP;⑤S四边形AEPF=S△APC.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),其中正确的序号有________________.
【答案】①②③⑤
【解析】∵AB=AC,∠BAC=90°,点P是BC的中点,
∴AP⊥BC,AP=PC,∠EAP=∠C=45°,
∴∠APF+∠CPF=90°,
∵∠EPF是直角,
∴∠APF+∠APE=90°,∴∠APE=∠CPF,故②正确,
在△APE和△CPF中,
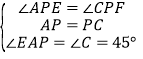 ,
,
∴△APE≌△CPF(ASA),
∴AE=CF,故①正确,∴△EFP是等腰直角三角形,故③正确,
根据等腰直角三角形的性质,EF=![]() PE,
PE,
所以,EF随着点E的变化而变化,只有当点E为AB的中点时,EF=![]() PE=AP,
PE=AP,
在其它位置时EF≠AP,故④错误,
∵△APE≌△CPF,
∴S△APE=S△CPF,
∴S四边形AEPF=S△APF+S△APE=S△APF+S△CPF=S△APC=![]() S△ABC,故⑤正确,综上所述,故答案为:①②③⑤.
S△ABC,故⑤正确,综上所述,故答案为:①②③⑤.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知数轴上A,B两点对应的数分别为-2,4,点P为数轴上一动点,其对应的数为x.
![]()
(1)若点P到点A,B的距离相等,求点P对应的数x的值.
(2)数轴上是否存在点P,使点P到点A,B的距离之和为8?若存在,请求出x的值;若不存在,说明理由.
(3)点A,B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以5个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间.当点A与点B重合时,点P经过的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两个全等的矩形,如果用彩色胶带按如图所示的方式包扎礼盒,那么所需胶带长度至少为多少厘米?(结果精确到1 cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景点的团体购买门票票价如下:

今有甲、乙两个旅行团,已知甲团人数少于 50 人,乙团人数不超过 100 人.若分别购票,两团共计应付门票费 1950 元,若合在一起作为一个团体购票,总计应付门票 费 1545 元.
(1)请你判断乙团的人数是否也少于 50 人;
(2)求甲、乙两旅行团各有多少人?
(3)甲旅行团单独购票,有无更省钱的方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.

(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是___个单位长度;△AOC与△BOD关于直线对称,则对称轴是___;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___度;
(2)连结AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富群众的业余生活并迎接社区文艺汇演,某小区特组建了一支“大妈广场舞队”(人数不超过50人).排练时,若排7排,则多3人;若排9排,且每排人数仅比排7 排时少1人,则最后-排不足6人.
(1)该“大妈广场舞队”共有多少名成员?
(2)为了提升表演效果,领队决定购买扇子和鲜花作为“大妈广场舞队”的表演道具.经预算,如果给40%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费558元;如果 给60%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费612元.问扇子和 鲜花的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
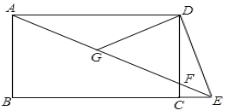
【题目】如图,点E是矩形ABCD的边BC延长线上一点,连接AE,交CD于点F,G是AF的中点,再连接DG、DE,且DE=DG.
(1)求证:∠DEA=2∠AEB;
(2)若BC=2AB,求∠AED的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com