
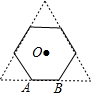
 如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.分析 (1)根据题意和正六边形的性质求出正六边形的边长;
(2)求出正六边形的中心角,根据正弦的概念解答即可;
(3)根据题意画出图形,根据圆的面积公式计算即可.
解答 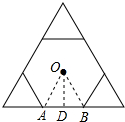 解:(1)∵正三角形的边长为6cm,
解:(1)∵正三角形的边长为6cm,
∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2;
(2)连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB=$\frac{360°}{6}$=60°,
∴△OAB是等边三角形,
∴OD=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$;
(3)如图2: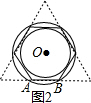
线段AB划过的面积=π×22-π×($\sqrt{3}$)2=πcm2.
点评 本题考查的是正多边形和圆的有关计算,正多边形的半径:外接圆的半径叫做正多边形的半径.中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.边心距:中心到正多边形的一边的距离叫做正多边形的边心距,正确运用三角函数或勾股定理进行计算是解题的关键.


科目:初中数学 来源: 题型:选择题
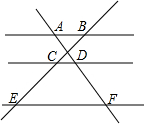 如图,已知AB∥CD∥EF,那么下列结论不正确的是( )
如图,已知AB∥CD∥EF,那么下列结论不正确的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CE}{EB}=\frac{DF}{AF}$ | D. | $\frac{BC}{BE}=\frac{AD}{AF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
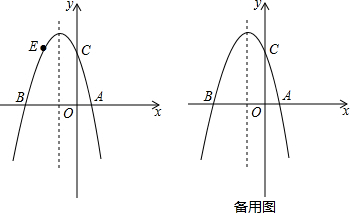
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
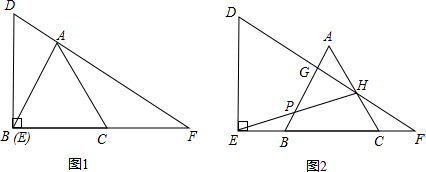
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com