
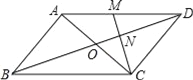
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
【答案】(1)6;(2)5.
【解析】试题分析:(1)、由四边形ABCD为平行四边形,得到对边平行且相等,且对角线互相平分,根据两直线平行内错角相等得到两对角相等,进而确定出三角形MND与三角形CNB相似,由相似得比例,得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;(2)、由相似三角形相似比为1:2,得到S△MND:S△CND=1:4,可得到△MND面积为1,△MCD面积为3,由S平行四边形ABCD=ADh,S△MCD=MDh=ADh,=4S△MCD,即可求得答案.
试题解析:(1)、∵平行四边形ABCD, ∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC, ∴△MND∽△CNB, ∴![]() ,
,
∵M为AD中点,所以BN=2DN, 设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1), 解得:x=3, ∴BD=2x=6;
(2)、∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=1:2, ∴S△MND:S△CND=1:4, ∵△DCN的面积为2, ∴△MND面积为1,
∴△MCD面积为3, 设平行四边形AD边上的高为h, ∵S平行四边形ABCD=ADh,S△MCD=MDh=ADh,
∴S平行四边形ABCD=4S△MCD=12. ∴四边形ABCM的面积=9.


科目:初中数学 来源: 题型:
【题目】某中学为了了解学生对手机的依赖程度,开展了一次“学生周末手机使用时间”抽样调查,根据调查结果绘制了如下两种不完整的统计图表.
组别 | 周末手机使用时间 | 人数 |
|
| 20 |
|
|
|
|
| 22 |
|
| 10 |
|
| 8 |
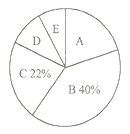
请根据图表信息解答下列问题:
(1)本次抽样,共调查了 人;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是/span> ;
”所对应的圆心角的度数是/span> ;
(3)估计该校2450名学生中周末手机使用时间小于2小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
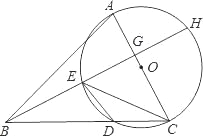
【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧![]() 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
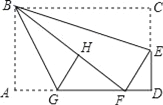
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明和父母一起开车到距家![]() 的景点旅游,出发前,汽车油箱内储油
的景点旅游,出发前,汽车油箱内储油![]() ,当行驶
,当行驶![]() 时,发现油箱余油量为
时,发现油箱余油量为![]() (假设行驶过程中汽车的耗油量是均匀的).
(假设行驶过程中汽车的耗油量是均匀的).
(1)这个变化过程中哪个是自变量?哪个是因变量?
(2)求该车平均每千米的耗油量,并写出行驶路程![]() 与剩余油量
与剩余油量![]() 的关系式;
的关系式;
(3)当![]() 时,求剩余油量
时,求剩余油量![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,平行四边形ABCD的中心E的坐标为(2,0),若点A的坐标为(-2,1),则点C的坐标为( )
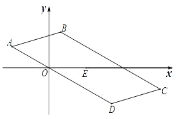
A. (4,-1)B. (6,-1)C. (8,-1)D. (6,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)如图1,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图2,若![]() 、
、![]() 分别为
分别为![]() ,
,![]() 延长线上的点,仍有
延长线上的点,仍有![]() ,其他条件不变,那么,
,其他条件不变,那么,![]() 是否仍为等腰直角三角形?证明你的结论.
是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com