
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() .
.
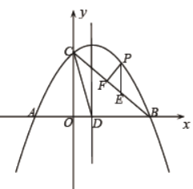
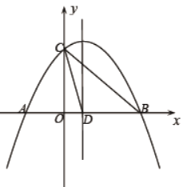
备用图
(1)求该抛物线的解析式;
(2)连接![]() ,能否在抛物线上找到一点
,能否在抛物线上找到一点![]() ,使得
,使得![]() ,若有求
,若有求![]() 点的坐标,若没有说明理由;
点的坐标,若没有说明理由;
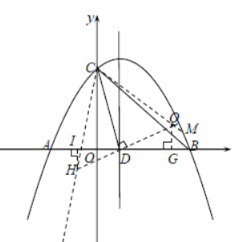
(3)若点![]() 为
为![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 的周长最大时,求点
的周长最大时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() ;(3)
;(3)![]()
【解析】
(1)由抛物线解析式可知点C坐标,由![]() 可知OB长,易得点B坐标,将点B坐标代入抛物线解析式可得该抛物线的解析式;
可知OB长,易得点B坐标,将点B坐标代入抛物线解析式可得该抛物线的解析式;
(2)分2种情况讨论,①若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,由作图可得
,由作图可得![]() 利用相似三角形对应线段成比例的性质及勾股定理可得点Q坐标,求出直线CQ的解析式,代入抛物线解析式易得点M坐标;②若
利用相似三角形对应线段成比例的性质及勾股定理可得点Q坐标,求出直线CQ的解析式,代入抛物线解析式易得点M坐标;②若![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据等边三角形三线合一,
,根据等边三角形三线合一,![]() ,则
,则![]() ,利用全等三角形的性质可得点H坐标,求出直线CH的解析式代入抛物线解析式可求得点M坐标;
,利用全等三角形的性质可得点H坐标,求出直线CH的解析式代入抛物线解析式可求得点M坐标;
(3)由题意可知![]() ,易知
,易知![]() ,当
,当![]() 的周长最大只需
的周长最大只需![]() 最大即可,求出
最大即可,求出![]() 所在直线的解析式,设
所在直线的解析式,设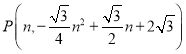 ,则
,则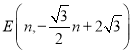 ,可表示出
,可表示出![]() ,易知当
,易知当![]() 时,
时,![]() 最大,即
最大,即![]() 的周长最大,把
的周长最大,把![]() 代入即可求出点P坐标.
代入即可求出点P坐标.
解:(1)![]() 抛物线
抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
![]()
![]() ,点
,点![]() 的坐标为
的坐标为![]()
把![]() 代入
代入![]() 得:
得:![]()
![]() 该抛物线的解析式为:
该抛物线的解析式为:![]()
(2)如图,若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]()
![]() 抛物线的对称轴交
抛物线的对称轴交![]() 轴于点
轴于点![]()
![]()
由作图可得:![]()
![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]() ,得
,得![]()
![]() ,可得:
,可得:![]()
![]() ,
,![]()
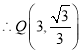
![]() 所在直线的解析式为:
所在直线的解析式为:![]()
把![]() 代入
代入![]() 解得:
解得:
![]() (舍去),
(舍去),![]()
把![]() 代入
代入![]()
得:![]()
![]()
另一种情况:如图,若![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据等边三角形三线合一,
,根据等边三角形三线合一,![]() ,
,
则![]()
![]() ,
,![]()
![]() ,
, ,
,
![]() 所在直线的解析式为:
所在直线的解析式为:![]()
把![]() 代入
代入![]() 解得:
解得:
![]() (舍去),
(舍去),![]()
把![]() 代入
代入![]() 得:
得:![]()
![]()
综上所述,满足条件的![]() 点有两个,分别为:
点有两个,分别为:
![]() 和
和![]()
(3)![]() 过点
过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
![]()
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]()
![]()
![]()
![]() 的周长最大只需
的周长最大只需![]() 最大即可,
最大即可,
![]() ,
,![]()
![]() 所在直线的解析式为:
所在直线的解析式为:![]()
![]() 点
点![]() 为
为![]() 上方抛物线上一动点,点
上方抛物线上一动点,点![]() 在
在![]() 上,且
上,且![]() 轴
轴
![]() 设
设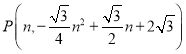 ,则
,则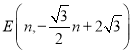
![]()
![]() 当
当![]() 时,
时,![]() 最大,即
最大,即![]() 的周长最大,
的周长最大,
把![]() 代入
代入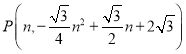 得:
得:
![]()
即当![]() 的周长最大时,点
的周长最大时,点![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,与抛物线
,与抛物线![]() 交于点
交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是线段
是线段![]() 上(不与
上(不与![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作矩形
为边作矩形![]() ,请求出矩形
,请求出矩形![]() 周长的最大值;
周长的最大值;
(3)若点![]() 在
在![]() 轴正半轴上,当
轴正半轴上,当![]() 恰好是等腰三角形时,请直接写出点
恰好是等腰三角形时,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
<>

请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
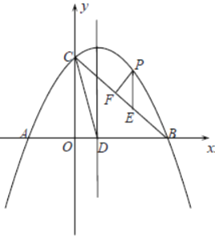
【题目】已知,如图,点P是平行四边形ABCD外一点,PE∥AB交BC于点E.PA、PD分别交BC于点M、N,点M是BE的中点.
(1)求证:CN=EN;
(2)若平行四边形ABCD的面积为12,求△PMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
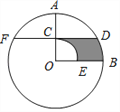
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.则图中阴影部分的面积为______________.
,交OB于E点.则图中阴影部分的面积为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )
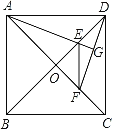
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
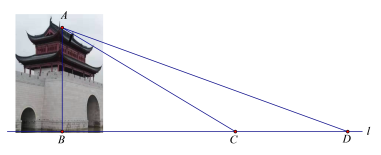
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com