
分析 首先根据题意画出图形,然后分别从BP=AB,AP=AB,AP=BP去分析求解即可求得答案.
解答  解:如图,∵A(-2,0),B(0,2),
解:如图,∵A(-2,0),B(0,2),
∴OA=2,OB=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$;
①若BP=AB=2$\sqrt{2}$,则OP1=BP-OB=2$\sqrt{2}$-2,OP2=BP+OB=2$\sqrt{2}$+1,
∴点P1(0,2-2$\sqrt{2}$),点P2(0,2+2$\sqrt{2}$);
②若AP=AB,则OP3=OB=2,
∴点P3(0,-2);
③若AP=BP,则P4与O重合,
∴点P4(0,0);
综上所述:点P的坐标是:(0,2-2$\sqrt{2}$),(0,2+2$\sqrt{2}$),(0,-2),(0,0).
故答案为:(0,2-2$\sqrt{2}$),(0,2+2$\sqrt{2}$),(0,-2),(0,0).
点评 此题考查了等腰三角形的性质.注意首先求得AB的长,然后利用分类讨论思想求解是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
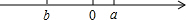 已知数a,b在数轴上对应点的位置如图所示,则下列结论正确的是②③④⑤⑥(填序号).
已知数a,b在数轴上对应点的位置如图所示,则下列结论正确的是②③④⑤⑥(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由一个平面图形得到它的轴对称图形叫作轴对称变换 | |
| B. | 将一个图形沿一条直线折叠叫作轴对称变换 | |
| C. | 对称轴方向和位置发生变化时,得到的图形方向和位置也发生变化 | |
| D. | 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com