
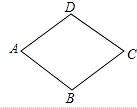
 如图,在菱形ABCD中,AB=5,∠BCD=120°,则菱形的面积为$\frac{25\sqrt{3}}{2}$.
如图,在菱形ABCD中,AB=5,∠BCD=120°,则菱形的面积为$\frac{25\sqrt{3}}{2}$. 分析 作AE⊥BC于E,在Rt△ABE中,由三角函数求出AE,即可得出菱形的面积.
解答 解:作AE⊥BC于E,如图所示:
∵四边形ABCD是菱形,∠BCD=120°,
∴AB=BC=5,∠ABC=60°,
∴AE=AB•sin60°=5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$,
∴菱形ABCD的面积=BC•AE=5×$\frac{5\sqrt{3}}{2}$=$\frac{25\sqrt{3}}{2}$;
故答案为:$\frac{25\sqrt{3}}{2}$.
点评 本题考查了菱形的性质、三角函数以及菱形面积的计算方法;通过解直角三角形求出菱形的高是解决问题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com