
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.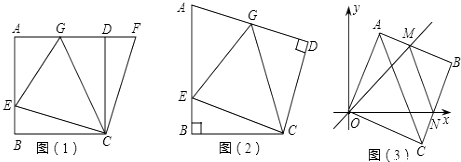
(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
【答案】
(1)
解:GE=BE+GD,理由如下:
∵四边形ABCD是正方形,F是AD延长线上一点,
∴BC=DC,∠FDC=∠EBC=90°,
在△EBC和△FDC中,  ,
,
∴△EBC≌△FDC(SAS),
∴∠DCF=∠BCE,CE=CF,
∵∠GCE=45°,
∴∠BCE+∠DCG=90°﹣45°=45°,
∴∠DCG+∠DCF=45°,
∴∠ECG=∠FCG,
在△ECG和△FCG中,  ,
,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∴GE=BE+GD
(2)
解:①α=2β时,GE=BE+GD;理由如下:
延长AD到F点,使DF=BE,连接CF,如图(2)所示:

∵∠B=∠D=90°,
∴∠B=∠FDC=90°,
在△EBC和△FDC中,  ,
,
∴△EBC≌△FDC(SAS),
∴∠DCF=∠BCE,CE=CF,
∴∠BCE+∠DCG=∠GCF,
当α=2β时,∠ECG=∠FCG,
在△ECG和△FCG中,  ,
,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∴GE=BE+GD;
②在旋转正方形OABC的过程中,P值无变化;
延长BA交y轴于E点,如图(3)所示:

则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN.
在△OAE和△OCN中, 
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中,  .
.
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.
∴在旋转正方形OABC的过程中,P值无变化.
【解析】(1)由SAS证得△EBC≌△FDC,再由SAS证得△ECG≌△FCG,可得到EG=FG,即可得出结果;(2)①延长AD到F点,使DF=BE,连接CF,可证△EBC≌△FDC,结合条件可证得△ECG≌△FCG,故EG=GF,可得出结论;②延长BA交y轴于E点,可证得△OAE≌△OCN,进一步可证得△OME≌△OMN,可求得MN=AM+AE


科目:初中数学 来源: 题型:
【题目】(1)若n为正整数,且a2n=3,计算(3a3n)2÷27a4n的值;
(2)已知(a-2)2+(b+2)2+(c-3)2=0,求![]() a2b3c4·(3ab2c2)2÷6(a2b3c4)2的值.
a2b3c4·(3ab2c2)2÷6(a2b3c4)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
(1)若将线段AB绕点O逆时针旋转90°得到线段A1B1 , 试在图中画出线段A1B1 .
(2)若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2 .
(3)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
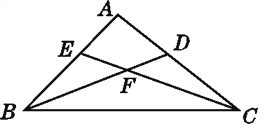
【题目】如图,以CD为公共边的三角形是____________;∠EFB是____________的内角;在△BCE中,BE所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P1(﹣1,y1),P2(﹣2,y2),P3(1,y3)都在函数y=x2﹣2x的图象上,则下列判断正确的是( )
A.y2<y1<y3B.y1<y2<y3C.y1>y2>y3D.y2>y1>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有3000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com