
·ÖĪö £Ø1£©Ö±½ÓĄūÓĆøÅĀŹ¹«Ź½Ēó½ā£»
£Ø2£©»Ź÷דĶ¼Õ¹Ź¾ĖłÓŠ9ÖÖµČæÉÄܵĽį¹ūŹż£¬ŌŁøł¾ŻµŚČżĻóĻŽµćµÄ×ų±źĢŲÕ÷ÕŅ³öµć£Øa£¬b£©ŌŚµŚČżĻóĻŽµÄ½į¹ūŹż£¬Č»ŗóøł¾ŻøÅĀŹ¹«Ź½Ēó½ā£®
½ā“š ½ā£ŗ£Ø1£©Ė껜µŲ“Ó²¼“üÖŠĆž³öŅ»øöŠ”Ēņ£¬ŌņĆž³öµÄĒņĪŖ±źÓŠŹż×Ö1µÄŠ”ĒņµÄøÅĀŹ=$\frac{1}{3}$£»
¹Ź“š°øĪŖ$\frac{1}{3}$£»
£Ø2£©»Ź÷דĶ¼£ŗ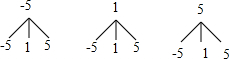
¹²ÓŠ9ÖÖµČæÉÄܵĽį¹ūŹż£¬ĘäÖŠ×ų±źµć£Øa£¬b£©ŌŚµŚČżĻóĻŽµÄ½į¹ūŹżĪŖ1£¬
ĖłŅŌ×ų±źµć£Øa£¬b£©ŌŚµŚČżĻóĻŽµÄøÅĀŹ=$\frac{1}{9}$£®
µćĘĄ ±¾Ģāæ¼²éĮĖĮŠ±ķ·ØÓėŹ÷דĶ¼·Ø£ŗĄūÓĆĮŠ±ķ·Ø»ņŹ÷דĶ¼·ØÕ¹Ź¾ĖłÓŠµČæÉÄܵĽį¹ūn£¬ŌŁ“ÓÖŠŃ”³ö·ūŗĻŹĀ¼žA»ņBµÄ½į¹ūŹżÄæm£¬Č»ŗóĄūÓĆøÅĀŹ¹«Ź½¼ĘĖćŹĀ¼žA»ņŹĀ¼žBµÄøÅĀŹ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
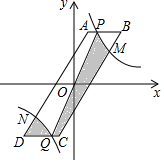 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬?ABCDµÄ¶Ō³ĘÖŠŠÄŹĒŌµćO£¬µćA”¢DµÄ×ų±ź·Ö±šĪŖ£Ø1£¬3£©”¢£Ø-3£¬-3£©£¬¶ÆµćPŌŚ±ßABÉĻ£¬¹żµćPµÄ·“±ČĄżŗÆŹży=$\frac{k}{x}$µÄĶ¼Ļó½»±ßCDÓŚµćQ£¬Į¬½ÓPQ£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬?ABCDµÄ¶Ō³ĘÖŠŠÄŹĒŌµćO£¬µćA”¢DµÄ×ų±ź·Ö±šĪŖ£Ø1£¬3£©”¢£Ø-3£¬-3£©£¬¶ÆµćPŌŚ±ßABÉĻ£¬¹żµćPµÄ·“±ČĄżŗÆŹży=$\frac{k}{x}$µÄĶ¼Ļó½»±ßCDÓŚµćQ£¬Į¬½ÓPQ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2·Ö | B£® | 4·Ö | C£® | 6·Ö | D£® | 8·Ö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
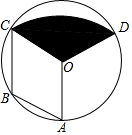 ČēĶ¼£¬µćA”¢B”¢CŌŚ”ŃOÉĻ£¬µćBŹĒ$\widehat{AC}$µÄÖŠµć£¬”ĻABC=”ĻAOC£¬½«ĖıߊĪAOCBČʵćA°“Ė³Ź±Õė·½ĻņŠż×ŖŅ»¶Ø½Ē¶Čŗ󣬵ćCĀäŌŚŌ²ÉĻµÄµćD“¦£¬Į¬½įOD£®
ČēĶ¼£¬µćA”¢B”¢CŌŚ”ŃOÉĻ£¬µćBŹĒ$\widehat{AC}$µÄÖŠµć£¬”ĻABC=”ĻAOC£¬½«ĖıߊĪAOCBČʵćA°“Ė³Ź±Õė·½ĻņŠż×ŖŅ»¶Ø½Ē¶Čŗ󣬵ćCĀäŌŚŌ²ÉĻµÄµćD“¦£¬Į¬½įOD£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
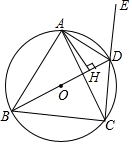 ČēĶ¼£¬BDŹĒ”ŃOµÄÖ±¾¶£¬ĖıߊĪABCDŹĒ”ŃOµÄÄŚ½ÓĖıߊĪ£¬ĒŅAB=AC£¬AH”ĶBDÓŚµćH£¬ŃÓ³¤CDÖĮµćE£®
ČēĶ¼£¬BDŹĒ”ŃOµÄÖ±¾¶£¬ĖıߊĪABCDŹĒ”ŃOµÄÄŚ½ÓĖıߊĪ£¬ĒŅAB=AC£¬AH”ĶBDÓŚµćH£¬ŃÓ³¤CDÖĮµćE£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 0.52”Į10-5 | B£® | 5.2”Į10-5 | C£® | 5.2”Į10-6 | D£® | 52”Į10-5 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com