
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
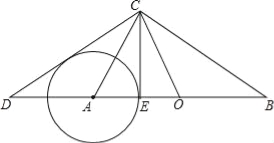
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
【答案】(1)详见解析;(2)(i)CE=6![]() ;(ii)详见解析.
;(ii)详见解析.
【解析】
试题分析:(1)因为∠ACB=∠DCO=90°,所以∠ACD=∠OCB,又因为点O是Rt△ACB中斜边AB的中点,所以OC=OB,所以∠OCB=∠B,利用等量代换可知∠ACD=∠B;(2)(i)因为BC2=ABBE,所以△ABC∽△CBE,所以∠ACB=∠CEB=90°,因为tan∠ACD=tan∠B,利用勾股定理即可求出CE的值;(ii)过点A作AF⊥CD于点F,易证∠DCA=∠ACE,即可得CA是∠DCE的平分线,所以AF=AE,所以直线CD与⊙A相切.
试题解析:(1)∵∠ACB=∠DCO=90°,
∴∠ACB﹣∠ACO=∠DCO﹣∠ACO,
即∠ACD=∠OCB,
又∵点O是AB的中点,
∴OC=OB,
∴∠OCB=∠B,
∴∠ACD=∠B,
(2)(i)∵BC2=ABBE,
∴![]() ,
,
∵∠B=∠B,
∴△ABC∽△CBE,
∴∠ACB=∠CEB=90°,
∵∠ACD=∠B,
∴tan∠ACD=tan∠B=![]() ,
,
设BE=4x,CE=3x,
由勾股定理可知:BE2+CE2=BC2,
∴(4x)2+(3x)2=100,
∴解得x=2![]() ,
,
∴CE=6![]() ;
;
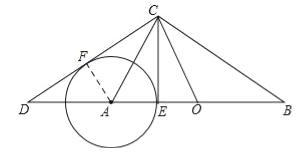
(ii)过点A作AF⊥CD于点F,
∵∠CEB=90°,
∴∠B+∠ECB=90°,
∵∠ACE+∠ECB=90°,
∴∠B=∠ACE,
∵∠ACD=∠B,
∴∠ACD=∠ACE,
∴CA平分∠DCE,
∵AF⊥CE,AE⊥CE,
∴AF=AE,
∴直线CD与⊙A相切.


科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AB=2 BC=4,点E、F分别是BC、AD的中点.
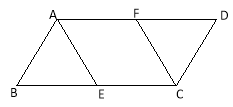
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一幅直角三角板叠放在一起,使直角顶点重合于点O. 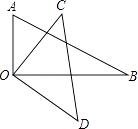
(1)若∠AOC=35°,求∠AOD的度数;
(2)问:∠AOC=∠BOD吗?说明理由;
(3)写出∠AOD与∠BOC所满足的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com