
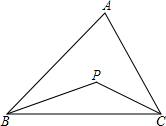
 如图,△ABC的两内角平分线交于点P.
如图,△ABC的两内角平分线交于点P.分析 (1)根据三角形内角和定理和角平分线的定义求出∠PBC+∠PCB的度数,根据三角形内角和定理求出∠BPC的度数;
(2)作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,根据角平分线的性质和判定证明即可.
解答 解:(1)∵∠BAC=110°,
∴∠ABC+∠ACB=180°-∠BAC=70°,
∵BP、CP是△ABC的两内角平分线,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=35°,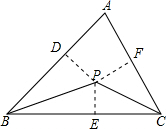 ∴∠BPC=180°-(∠PBC+∠PCB)=145°,
∴∠BPC=180°-(∠PBC+∠PCB)=145°,
故答案为:145°;
(2)作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BP、CP是△ABC的两内角平分线,
∴PD=PE,PF=PE,
∴PD=PF,又PD⊥AB,PF⊥AC,
∴点P在∠BAC的平分线上.
点评 本题考查的是角平分线的定义和性质以及三角形内角和定理,掌握角的平分线上的点到角的两边的距离相等、到角的两边的距离相等的点在角的平分线上是解题的关键.


科目:初中数学 来源: 题型:解答题
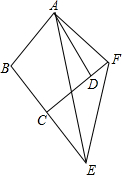 如图.在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,求证:EF=BE-FD.
如图.在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,求证:EF=BE-FD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
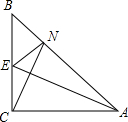 如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
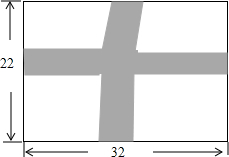 如图,花园中间有两条小路,小路的两个边界完全相同,且任何地方的水平宽度都相同,已知除去小路后的花园面积为600平方米.如果设计小路的宽度为x米,为求小路的宽度可列方程为x2-52x+40=0.
如图,花园中间有两条小路,小路的两个边界完全相同,且任何地方的水平宽度都相同,已知除去小路后的花园面积为600平方米.如果设计小路的宽度为x米,为求小路的宽度可列方程为x2-52x+40=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com