
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF. 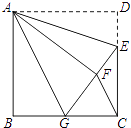
(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
【答案】
(1)证明:①在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴△ABG≌△AFG(HL);
②∵CD=3DE
∴DE=2,CE=4,
设BG=x,则CG=6﹣x,GE=x+2
∵GE2=CG2+CE2
∴(x+2)2=(6﹣x)2+42,
解得x=3,
∴CG=6﹣3=3;
(2)解:如图,过C作CM⊥GF于M,
∵BG=GF=3,
∴CG=3,EC=6﹣2=4,
∴GE= ![]() =5,
=5,
CMGE=GCEC,
∴CM×5=3×4,
∴CM=2.4,
∴S△FGC= ![]() GF×CM=
GF×CM= ![]() ×3×2.4=3.6.
×3×2.4=3.6.
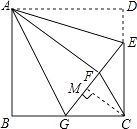
【解析】(1)①利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;②利用勾股定理得出GE2=CG2+CE2 , 进而求出BG即可;(2)首先过C作CM⊥GF于M,由勾股定理以及由面积法得,CM=2.4,进而得出答案
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】下列各组线段中,能组成三角形的是( )
A. a=3 cm,b=8 cm,c=5 cm
B. a=5 cm,b=5 cm,c=10 cm
C. a=12 cm,b=5 cm,c=6 cm
D. a=15 cm,b=10 cm,c=7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线
经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线![]() :
:![]() (a≠0),
(a≠0),
(1)试求抛物线![]() 的函数解析式;
的函数解析式;
(2)求证: 抛物线 ![]() 与x轴一定有两个不同的交点;
与x轴一定有两个不同的交点;
(3)若a=1
①抛物线![]() 、
、![]() 顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线
顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线![]() 、
、![]() 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;
②已知直线MN分别与x轴、![]() 、
、![]() 分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起, 
(1)若∠DCE=25°,∠ACB=;若∠ACB=150°,则∠DCE=;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD. 
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y1=x+1的图象与x轴交于点A,与反比例函数![]() 的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
(1)请直接写出在第一象限内,当x取何值时,y1>y2?
(2)将线段BC沿一次函数的图象平移至点B与点A重合,平移后点C的对应点是否在反比例函数的图象上?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com