Question

15．如图，在平面直角坐标系中，抛物线y=-$\frac{4}{9}$x²+$\frac{8}{3}$x的顶点为A，与x轴交于点B，点D是线段OB上的动点，沿O到B的方向运动，∠ADC交AB于点C，且∠ADC=∠AOB．

（1）求点A，点B的坐标及OA的长；
（2）求在点D运动的过程中，线段BC的最大值；
（3）探究：在点D运动过程中，△ADC是否会成等腰三角形？若能，求出点D的坐标；若不能，请说明理由．

Answer 1

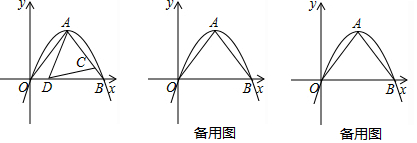
分析 （1）令y=0求出B点坐标，；于配方法求出点A的坐标即可．
（2）首先证明△OAD∽△BDC，得$\frac{OD}{OA}$=$\frac{BC}{BD}$，设OD=x，则DB=6-x，得$\frac{x}{5}$=$\frac{BC}{6-x}$，所以BC=-$\frac{1}{5}$x²+$\frac{6}{5}$x，利用二次函数的性质即可解决问题．
（3）分三种情形）①当AD=AC时，则∠CDA=∠ACD，不可能．②当AD=CD时，则△OAD≌△BDC，③当AC=DC时，可得△ABD∽△OBA，分别求出OD即可．

解答 解：（1）对于抛物线y=-$\frac{4}{9}$x²+$\frac{8}{3}$x，令y=0，得到-$\frac{4}{9}$x²+$\frac{8}{3}$x=0，解得x=0或6，
∴B（6，0），
∵y=-$\frac{4}{9}$x²+$\frac{8}{3}$x=-$\frac{4}{9}$（x²-6x）=-$\frac{4}{9}$（x-3）²+4，
∴A（3，4），
OA=$\sqrt{{3}^{2}+{4}^{2}}$=5．

（2）根据对称性OA=AB=5，
∴∠AOD=∠ABO，
∵∠ADB=∠CDB+∠ADC=∠AOD+∠OAD，∠ADC=∠AOD，
∴∠CDB=∠OAD，
∴△OAD∽△BDC，
∴$\frac{OD}{OA}$=$\frac{BC}{BD}$，设OD=x，则DB=6-x，
∴$\frac{x}{5}$=$\frac{BC}{6-x}$，
∴BC=-$\frac{1}{5}$x²+$\frac{6}{5}$x=-$\frac{1}{5}$（x-3）²+$\frac{9}{5}$，
∵-$\frac{1}{5}$＜0，
∴x=3时，BC的最大值为$\frac{9}{5}$．

（3）①当AD=AC时，则∠CDA=∠ACD，不可能．
②当AD=CD时，则△OAD≌△BDC，
∴DB=OA=5，
∴D₁（1.0）．
③当AC=DC时，∠CDA=∠CAD，
∵∠CDA=∠AOB，
∴∠CAD=∠AOB，∠ABD=∠OBA，
∴△ABD∽△OBA，
∴$\frac{DB}{AB}$=$\frac{AB}{OB}$，设DB=y，则$\frac{y}{5}$=$\frac{5}{6}$，
∴y=$\frac{25}{6}$，
∴OD=OB-BD=6-$\frac{25}{6}$=$\frac{11}{6}$，
∴D₂（$\frac{11}{6}$，0），
综上所述，符合条件的点有D₁（1，0）或（$\frac{11}{6}$，0）．

点评 本题考查二次函数综合题、待定系数法、等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识，学会用分类讨论的首先思考问题，注意不能漏解．属于中考压轴题．