Question

1．如图所示，直角三角板ABC放置于直角坐标系中，已知点B（0，2），点A（4，5），点C在第四象限，∠A=60°，∠C=30°，BC边与x轴交于点D．
（1）求AB的长度；
（2）求点C的坐标．

Answer 1

分析 （1）过点A作AE⊥y轴于点E，根据A、B坐标求得AE、BE的长，继而根据勾股定理可得AB 的长；
（2）过C作CF⊥y轴于点F，先求出BC的长，再证△BFC∽△AEB得$\frac{CF}{BE}=\frac{BF}{AE}=\frac{BC}{AB}$，可求得CF、BF，继而可得OF=BF-OB=$4\sqrt{3}-2$，即可得答案．

解答 解：（1）过点A作AE⊥y轴于点E，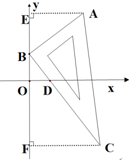

∵点A（4，5），B（0，2），
∴AE=4，BE=5-2=3，
由勾股定理得：$AB=\sqrt{B{E^2}+A{E^2}}=\sqrt{{3^2}+{4^2}}$=5；

（2）在Rt△ABC中，∵∠A=60°，AB=5，
∴BC=AB tan 60°=5$\sqrt{3}$，
过C作CF⊥y轴于点F，
则∠BFC=∠AEB=90°
∵∠CBF+∠ABE=90°，∠CBF+∠BCF=90°
∴∠BCF=∠ABE，
∴△BFC∽△AEB，
∴$\frac{CF}{BE}=\frac{BF}{AE}=\frac{BC}{AB}$，即$\frac{CF}{3}=\frac{BF}{4}=\frac{{5\sqrt{3}}}{5}$，
∴$CF=3\sqrt{3}，BF=4\sqrt{3}$，
∵OF=BF-OB=$4\sqrt{3}-2$
∴点C的坐标为（$3\sqrt{3}$，$2-4\sqrt{3}$）．

点评 本题主要考查勾股定理和相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．