
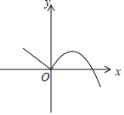
【题目】已知函数y= 的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为_____.
的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为_____.
【答案】0<m<![]()
【解析】
由直线y=x+m与该图象恰有三个不同的交点可知直线y=x+m与y=-x(x≤0)有一个交点,与y=-x2+2x有两个交点,分别联立两个解析式求出m的取值范围即可得答案.
∵直线y=x+m与该图象恰有三个不同的交点,
∴直线y=x+m与y=-x(x≤0)有一个交点,与y=-x2+2x(x>0)有两个交点,
x+m=-x
x=![]() ,
,
∵x≤0,
∴m≥0,
-x2+2x=x+m,
x2-x+m=0,
∵y=x+m与y=-x2+2x(x>0)有两个交点,
∴△=(-1)2-4m>0,
解得:m<![]() ,
,
∵当m=0时,直线y=x+m过(0,0)点,
∴与y=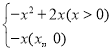 图象只有两个交点,
图象只有两个交点,
∴m≠0,
∴m的取值范围为:0<m<![]() .
.
故答案为:0<m<![]()


科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 是正方形,且
是正方形,且![]() ,点
,点![]() 与
与![]() 重合,以
重合,以![]() 为圆心,作半径长为5的半圆
为圆心,作半径长为5的半圆![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
发现![]() 是半圆
是半圆![]() 上任意一点,连接
上任意一点,连接![]() ,则
,则![]() 的最大值为______;
的最大值为______;
思考如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转,记旋转角为
逆时针旋转,记旋转角为![]()
(1)当![]() 时,求半圆
时,求半圆![]() 落在正方形内部的弧长;
落在正方形内部的弧长;
(2)在旋转过程中,若半圆![]() 与正方形
与正方形![]() 的边相切时,请直接写出此时点
的边相切时,请直接写出此时点![]() 到切点的距离.(注:
到切点的距离.(注:![]() ,
,![]() ,
,![]() )
)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
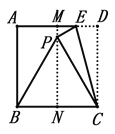
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级举行了“中国梦”演讲比赛活动,学校团委根据学生的成绩划分为A,B,C,D四个等级,并绘制了如下两个不完整的两种统计图.

根据图中提供的信息,回答下列问题
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ;C等级对应的扇形的圆心角为 度.
(3)学校准备从获得A等级的学生中随机选取2人,参加全市举办的演讲比赛,请利用列表法或树状图法,求获得A等级的小明参加市比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=4,AB=5,点E、F分别在AC、AB上,连接EF,将△ABC沿EF折叠,使点A落在BC边上的点D处.若△DEF有一边垂直BC,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙二人走步晨练,两人同时同地向距离600米的目标出发,二人所走的路程y(米)与所走的时间t(分)之间的函数关系如图所示,下列说法:①甲走全程的平均速度为75米/分:②第4分钟时,二人在途中相遇;③第2分钟时甲在乙前面100米处;④乙比甲提前2.5分钟到达终点;其中正确的有( )个.

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全区3000名九年级学生英语听力口语自动化考试成绩的情况,随机抽取了部分学生的成绩(满分30分且得分均为整数),制成下表:
分数段(x分分) | 0≤x≤18 | 19≤x≤21 | 22≤x≤24 | 25≤x≤27 | 28≤x≤30 |
人数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数所在的分数段是 ;
③若用扇形统计图表示统计结果,则分数段为0≤x≤18的人数所对应扇形的圆心角为 °;
(2)如果将25分以上(含25分)定为优秀,请估计全区九年级考生成绩为优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
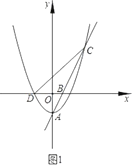
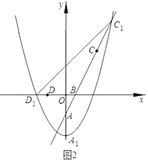
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com