
分析 (1)先化简题目中的二次根式,然后根据二次根式的加减法和乘除法即可解答本题;
(2)根据平方差公式和完全平方公式可以解答本题.
解答 解:(1)($\sqrt{20}$+$\sqrt{5}$)÷$\sqrt{5}$-$\sqrt{\frac{1}{3}}$×12
=$(2\sqrt{5}+\sqrt{5})÷\sqrt{5}-\frac{\sqrt{3}}{3}×12$
=$3\sqrt{5}÷\sqrt{5}-4\sqrt{3}$
=3-4$\sqrt{3}$;
(2)($\sqrt{5}$-$\sqrt{3}$)($\sqrt{5}$+$\sqrt{3}$))-${(\sqrt{2}+\sqrt{6})}^{2}$
=5-3-(2+4$\sqrt{3}$+6)
=5-3-8-4$\sqrt{3}$
=-6-4$\sqrt{3}$.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式的混合运算的计算方法.


科目:初中数学 来源: 题型:解答题
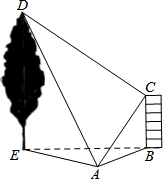 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.
如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,求树高DE的长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
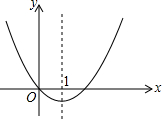 二次函数y=x2+bx的图象如图,对称轴为直线x=1.若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8..
二次函数y=x2+bx的图象如图,对称轴为直线x=1.若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8..查看答案和解析>>
科目:初中数学 来源: 题型:填空题
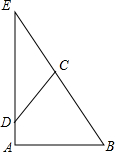 如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.
如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面的推理过程.
完成下面的推理过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
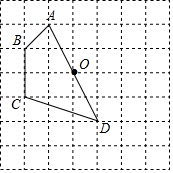 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com