
��ͼ����ƽ��ֱ�������У���A������Ϊ��1��1����OA=AC����OAC=90�㣬��DΪx����һ���㣮��ADΪ����AD���Ҳ���������ADEF��
��1������D���߶�OC��ʱ�������O��C�غϣ������߶�CF��OD֮���������ϵΪ ��λ�ù�ϵΪ ��
��2������D���߶�OC���ӳ�����ʱ����1���еĽ����Ƿ����������������˵�����ɣ��������������һ������
��3����D������Ϊ��t��0������D���O���˶���C��ʱ���ú�t�Ĵ���ʽ��ʾE�����꣬��ֱ��д��E����������·������
��1����ȡ���ֱ����2�����۳�������3��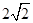 ��
��
�������������
��1����ȡ���ֱ
��2�����۳���
֤������OA=AC����OAC=90�㣬�ı���ADEFΪ������
���OAD=��CAF��AD=AF
���AOD��ACF
��OD=CF
��ACF=AOD=45��
�ߡ�ACO=45�㣬���OCF=90�㣬��CF��OD
��3����A����AH��x�ᣬHΪ���㣬��E��EM��x����M
���ADH=��DEM����AHD=��DME=90�㣬AD=DE��
���ADH�ա�DEM
��AH=DM=1��DH=ME=1-t
��E��1+t��t-1����0��t��2��
��x=1+t��y=t-1
��y=x-2
��E��ֱ��y=x-2���˶���1��x��3
��E������·����Ϊ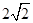 ��
��
���㣺1�������ε����ʣ�2��ȫ�������ε��ж������ʣ�3��һ�κ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��װ��˾����һ�ֳɱ�Ϊÿ��50Ԫ��T�������涨����ʱ�����۵��۲����ڳɱ��ۣ��ֲ�����ÿ��70Ԫ��������������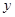 �����������۵���
�����������۵��� ��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��1����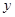 ��
�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���蹫˾��õ�������������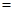 �����۶�
�����۶�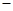 �ܳɱ���Ϊ
�ܳɱ���Ϊ Ԫ����
Ԫ���� ��
�� ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա��� ��ȡֵ��Χ�����������жϣ���
��ȡֵ��Χ�����������жϣ��� ȡ��ֵʱ��
ȡ��ֵʱ�� ��ֵ������ֵ�Ƕ��٣�
��ֵ������ֵ�Ƕ��٣�
��3������˾Ҫ��֤�����ܵ���4000Ԫ�������۵���x��ȡֵ��ΧΪ����Ԫ���ɽ������κ�����ͼ���𣩣� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�졢�������ֱ�����360ǧ��·�̵ļס�������ͬʱ������������ʻ����������У��쳵�����ҵغ�ͣ��1Сʱ��Ȼ��ԭ·ԭ�ٷ��أ��쳵��������1Сʱ����أ��졢����������Գ����ص�·��y(ǧ��)����������õ�ʱ��x(Сʱ)�Ĺ�ϵ��ͼ��ʾ��
����ͼ����Ϣ����������⣺
(1)�������ٶ��� ǧ�ף�Сʱ���쳵���ٶ��� ǧ�ף�Сʱ��
(2)��m��ֵ����ָ����C��ʵ��������ʲô��
(3)�ڿ쳵��ԭ·ԭ�ٷ��صĹ����У��졢����������·��Ϊ150ǧ��ʱ��������ʻ�˶���Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�������鹤��ͬʱ��ʼ�ӹ�ij������������ڹ�������һ��ͣ�������豸�������豸������Ĺ���Ч����ԭ����2��.������Լӹ����������y��������ʱ��x��ʱ��֮�亯��ͼ����ͼ��ʾ��
��1��������y��ʱ��x֮�亯����ϵʽ��
��2��������ӹ��������aֵ��
��3����������ӹ������������һ��װ�䣬ÿ��300��װһ�䣬װ��ʱ����Բ��ƣ����ʱ��ǡ��װ����1�䣿�پ����ʱ��ǡ��װ����2�䣿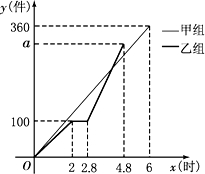
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪���������� ��x > 0��k�dz�������ͼ����A��1,4������B��m , n��������m��1�� AM��x�ᣬ����ΪM��BN��y�ᣬ����ΪN��AM��BN�Ľ���ΪC��
��x > 0��k�dz�������ͼ����A��1,4������B��m , n��������m��1�� AM��x�ᣬ����ΪM��BN��y�ᣬ����ΪN��AM��BN�Ľ���ΪC��
��1��д����������������ʽ��
��2����֤��∆ACB��∆NOM��
��3����∆ACB��∆NOM�����Ʊ�Ϊ2�����B������꼰AB����ֱ�ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��һ��ֱ����������A��B��C���أ����г������ס�������ͬʱ�ֱ��A��B���س�������ֱ����������C�أ���֪���ٶ�Ϊ20 km/h����ס���������ʻx��h������A�صľ���ֱ�Ϊy1��y2 ��km���� y1��y2 ��x�ĺ�����ϵ��ͼ��ʾ��
��1����y2��x�ĺ�����ϵʽ��
��2���������ڳ���ʱ���䱸��ͨ������Ϊ3km�ĶԽ�������ס������������й����п����öԽ���ͨ����ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ͼ������������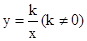 ��һ�κ���
��һ�κ���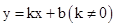 ��ͼ����A��3,1����B��m��-3������.
��ͼ����A��3,1����B��m��-3������.
��1����������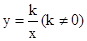 ��һ�κ���
��һ�κ���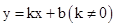 �Ľ���ʽ.
�Ľ���ʽ.
��2������P��ֱ��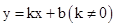 ��һ�㣬��OP=
��һ�㣬��OP= OA����ֱ��д����P������.
OA����ֱ��д����P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�٣���ƽ���ı���ABCD�У�AB=13��BC=50��BC���ϵĸ�Ϊ12����P�ӵ�B��������B��A��D��A�˶�����B��A�˶�ʱ���ٶ�Ϊÿ��13����λ���ȣ���A��D��A�˶�ʱ���ٶ�Ϊÿ��8����λ���ȣ���Q�ӵ�B������BC�����˶����ٶ�Ϊÿ��5����λ���ȣ�P��Q����ͬʱ����������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt���룩������PQ��
��1������P��A��D��A�˶�ʱ����AP�ij����ú�t�Ĵ���ʽ��ʾ����
��2������AQ���ڵ�P��B��A��D�˶������У�����P���B����A���غ�ʱ���ǡ�APQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��3������Q��QR��AB����AD�ڵ�R������BR����ͼ�ڣ��ڵ�P��B��A��D�˶������У����߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ�������ʱt��ֵ��
��4�����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬ֱ��д��C��D���BCʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��˾�м���ԭ��260kg������ԭ��270kg���ƻ���������ԭ������A��B���ֲ�Ʒ��40��������ÿ��A�ֲ�Ʒ�����ԭ��8kg������ԭ��5kg���ɻ�����900Ԫ������ÿ��B�ֲ�Ʒ�����ԭ��4kg������ԭ��9kg���ɻ�����1100Ԫ���谲������A�ֲ�Ʒx����
��1������±�
| | �ף�kg�� | �ң�kg�� | ���������� |
| A | | 5x | x |
| B | 4��40-x�� | | 40-x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com