
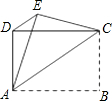
 如图,四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,已知DE:AC=5:13,则sin∠CAB=
如图,四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,已知DE:AC=5:13,则sin∠CAB=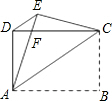 解:∵四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,
解:∵四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,| EF |
| FC |
| DF |
| AF |
| DF |
| AF |
| DE |
| AC |
| 5 |
| 13 |
| AF2-DF2 |
| AB2+BC2 |
| 13 |
| BC |
| AC |
| 12x | ||
6
|
2
| ||
| 13 |
2
| ||
| 13 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
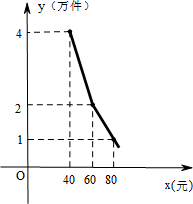 ,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点.
两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
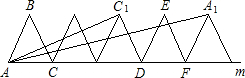 如图,已知边长为2的正三角形ABC沿直线m滚动,当△ABC滚动一周时,到△DEF位置.设△ABC滚动240°时,点C的位置为C1,△ABC滚动480°时,点A的位置为点A1.根据三角函数正切的两角和公式tan(α+β)=
如图,已知边长为2的正三角形ABC沿直线m滚动,当△ABC滚动一周时,到△DEF位置.设△ABC滚动240°时,点C的位置为C1,△ABC滚动480°时,点A的位置为点A1.根据三角函数正切的两角和公式tan(α+β)=| tanα+tanβ |
| 1-tanα•tanβ |
查看答案和解析>>
科目:初中数学 来源: 题型:
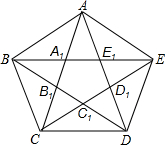 如图,在正五边形ABCDE中,对角线分别相交于点A1、B1、C1、D1、E1.将所有全等的三角形视为一类,称为一个“全等类”( 如△ABC、△BCD与△CDE等都属于同一个全等类).则图中不同全等类的个数为( )
如图,在正五边形ABCDE中,对角线分别相交于点A1、B1、C1、D1、E1.将所有全等的三角形视为一类,称为一个“全等类”( 如△ABC、△BCD与△CDE等都属于同一个全等类).则图中不同全等类的个数为( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com