
已知:直线y=x+6交x轴于A点,交y轴于C两点,经过A和原点O的抛物线y==ax2+bx(a<0)的顶点B在直线AC上。
(1)求点A、C、B的坐标
(2)求出抛物线的函数关系式;
(3)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并求出BD的长;
(4)若E为⊙B优弧 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由
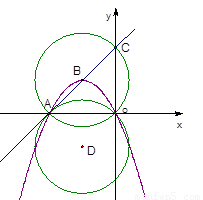
∵A(-6,0),C(0,6)
∴抛物线的对称轴是直线x=3,又B在AC上
∴抛物线的顶点是 B(-3,3)
(2)∴设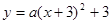 又过A(-6,0)
又过A(-6,0)
把A(-6,0)代入上式得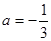
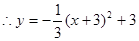
即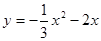
(2)∵⊙D与⊙O关于X轴对称
∴D(-3,-3)
∴BD=6
∵AD=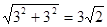 ,AB=
,AB=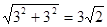
∴
∴∠BAD=
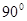
∴AC是⊙D的切线
(3)∵∠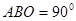
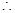 ∠AEO=
∠AEO=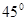
假设在抛物线上存在一点M(x,y),使得∠MOA:∠AEO=2:3
则∠MOA=300, 则M必在直线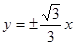 上
上
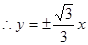
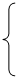


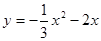 得
得 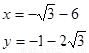
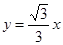
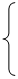
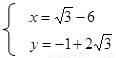
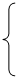
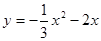
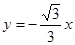
∴存在这样的M,M的坐标有两个:
M
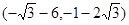

或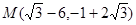
【解析】(1)根据过A、C两点的直线的解析式即可求出A,C的坐标.
(2)根据A,O的坐标即可得出抛物线的对称轴的解析式,然后将A点坐标代入抛物线中,联立上述两式即可求出抛物线的解析式.
(3)直线与圆的位置关系无非是相切与否,可连接AD,证AD是否与AC垂直即可.由于B,D关于x轴对称,那么可得出∠CAO=∠DAO=45°,因此可求出∠DAB=90°,即DA⊥AC,因此AC与圆D相切.
(4)根据圆周角定理可得出∠AEO=45°,那么∠MOA=30°,即M点的纵坐标的绝对值和横坐标的绝对值的比为tan30°,由此可得出x,y的比例关系式,然后联立抛物线的解析式即可求出M点的坐标.(要注意的是本题要分点M在x轴上方还是下方两种情况进行求解)


科目:初中数学 来源: 题型:
| n |
| n+1 |
| ||
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),
已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com