
| 3 |

| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
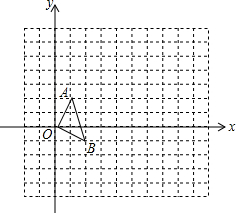 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).| 4 | 3 |

查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏南京卷)数学(带解析) 题型:解答题
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段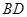 的长为
的长为  ;
;
(2)如图3,分别以锐角三角形 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形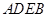 ,
, ,
, ,点
,点 ,
,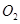 ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段 的长为
的长为  ;
;
(2)如图3,分别以锐角三角形 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com