练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    图甲中，正方形ABDE、CDFI、EFGH的面积分别为17，10，13，图乙中，DPQR为矩形，对照图乙，计算图甲中六边形ABCIGH的面积．

    解：∵DF=DC，DE=DB，且∠EDF+∠BDC=180°，
    根据三角形的面积公式得S△AHE=S△DEF，
    同理+S△BDC=S△GFI=S△DEF，
    S△AHE+S△BDC+S△GFI=3×S△DEF，
    S△DEF=3×4-2-3-1.5=5.5，
    ∴六边形ABCIGH的面积为S△AHE+S△BDC+S△GFI+S△DEF+17+13+10
    =62．
    答：六边形ABCIGH的面积为62．
    分析：求出△BCD，△GFI，△AEH的面积即可，△DEF的面积通过图乙求解，
    点评：本题考查了正方形各边相等，且各内角等于直角的性质，考查了三角形面积的计算，解本题的关键是找到+S△BDC+S△GFI=3×S△DEF．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．

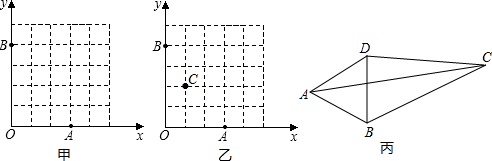
    （1）如图甲，已知格点（小正方形的顶点）O（0，0）A（3，0），B（0，4），请你画出以格点为顶点，OA、OB为勾股边且对角线相等的勾股四边形OAMB；
    （2）如图乙，若C（1，2），那么在图中所有格点中是否能找到一点D，使以CA、CB为勾股边的四边形ACBD是勾股四边形．如果能找到，请写出D点的坐标（不需要证明）；
    （3）如图丙，AC、BD是四边形ABCD的两条对角线，△ABD是等边三角形，∠DCB=30°．求证：四边形ABCD是勾股四边形．

    查看答案和解析>>

    同步练习册答案