沃尔玛在汉第五家门店安家黄陂广场,已于10月16开业.店内有一种新品牌的书包,已知其进价为每个30元,售价为每个40元时,平均每月能售出600个.调查表明:这种书包的售价每上涨1元(售价高于40元但不高于75元),其销售量就减少10个.设每月售出书包的利润为y(元),每个书包售价为x(元)(x为整数).
(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)每个书包的售价定为多少元时,每月利润最大?最大利润是多少?
(3)若商家想要获得10000元的月利润,则每个书包的售价定为多少元?
解:(1)由题意得
y=(40+x-30)(600-10x)=-10x
2+500x+6000,30≤x≤75;
(2)设利润为y元,得
y=(x-30)[600-10(x-40)],
即:y=-10x
2+1300x-30000.
∵a=-10<0
∴当x=-

=-

=65时,
y
最大=

=
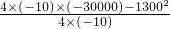
=12250.
答:售价为65元时,此时利润最大,最大为12250元.
(3)(x-30)[600-10(x-40)]=10000,
解得:x=50或x=80(不合题意舍去)
答:售价应定为50元.
分析:(1)设书包的售价为x元,由这种书包的售价每上涨1元,其销售量就减少10个,列出函数关系式;
(2)设利润为y元,列出二次函数关系式,求出最大值;
(3)令二次函数等于0,解得x的取值范围.
点评:此题主要考查了二次函数在实际生活中的应用,求出二次函数的最值问题是考查重点,同学们应熟练掌握.

 =-
=- =65时,
=65时, =
=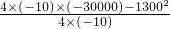 =12250.
=12250.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案