
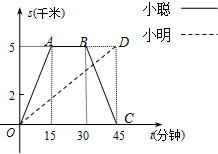
 小聪、小明两兄弟一起从家里出发到泉港区图书馆查阅资料,已知他们家到区图书馆的路程是5千米.小聪骑自行车,小明步行,当小聪从原路回到家时,小明刚好到达区图书馆.图中折线O-A-B-C和线段OD分别表示两人离家的路程S(千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:
小聪、小明两兄弟一起从家里出发到泉港区图书馆查阅资料,已知他们家到区图书馆的路程是5千米.小聪骑自行车,小明步行,当小聪从原路回到家时,小明刚好到达区图书馆.图中折线O-A-B-C和线段OD分别表示两人离家的路程S(千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:分析 (1)直接根据图象上所给的数据的实际意义可求解;
(2)由图象可知,s是t的正比例函数,设所求函数的解析式为s=kt(k≠0),把(45,5)代入解析式利用待定系数法即可求解;
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0),把(30,5),(45,0)代入利用待定系数法先求得函数关系式,再根据求函数图象的交点方法求得交点坐标即可.
解答 解:(1)由图象可知,小聪在泉港区图书馆查阅资料的时间为:30-15=15(分钟),
故答案为:15;
(2)由图象可知,s是t的正比例函数
设所求函数的解析式为s=kt(k≠0)
代入(45,5),得
5=45k
解得k=$\frac{1}{9}$,
故s与t的函数关系式s=$\frac{1}{9}$t(0≤t≤45);
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0)
代入(30,5),(45,0),得
$\left\{\begin{array}{l}{30m+n=5}\\{45m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=15}\end{array}\right.$.
∴s=-$\frac{1}{3}$t+15(30≤t≤45)
令-$\frac{1}{3}$t+15=$\frac{1}{9}$t,解得t=$\frac{135}{4}$,当t=$\frac{135}{4}$时,S=$\frac{1}{9}$×$\frac{135}{4}$=$\frac{15}{4}$.
答:当小聪与小明迎面相遇时,他们离家的路程是$\frac{15}{4}$千米.
点评 主要考查了一次函数的实际运用和读图能力.从图象中获得所需的信息是需要掌握的基本能力,还要会熟练地运用待定系数法求函数解析式和使用方程组求交点坐标的方法.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
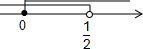 一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )| A. | 0<x≤$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | 0≤x<$\frac{1}{2}$ | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
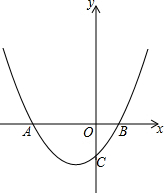 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+6ax-4与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴的负半轴相交于点C,且AB=10,一次函数y=x+b与抛物线相交于点E和点F(点E在点F左边),与抛物线的对称轴相交于点G.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+6ax-4与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴的负半轴相交于点C,且AB=10,一次函数y=x+b与抛物线相交于点E和点F(点E在点F左边),与抛物线的对称轴相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com