
| xy |
| x+y |
| 1 |
| 3 |
| yz |
| y+z |
| 1 |
| 5 |
| zx |
| z+x |
| 1 |
| 6 |
| xyz |
| xy+yz+zx |
A、
| ||
B、
| ||
C、
| ||
D、
|
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| xy |
| x+y |
| 1 |
| 3 |
| yz |
| y+z |
| 1 |
| 5 |
| zx |
| z+x |
| 1 |
| 6 |
| x+y |
| xy |
| 1 |
| x |
| 1 |
| y |
| y+z |
| yz |
| 1 |
| y |
| 1 |
| z |
| z+x |
| zx |
| 1 |
| z |
| 1 |
| x |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| xyz |
| xy+yz+zx |
| 1 | ||||||
|
| 1 |
| 7 |


科目:初中数学 来源: 题型:
| A、100m2 |
| B、1000m2 |
| C、10000m2 |
| D、100000m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、为检测我市正在销售的酸奶质量,应该采用抽样调查的方式 | ||
| B、两名同学连续五次数学测试的平均分相同,方差较大的同学数学成绩更稳定 | ||
C、抛掷一个正方体骰子,点数为奇数的概率是
| ||
| D、“打开电视,正在播放广告”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:
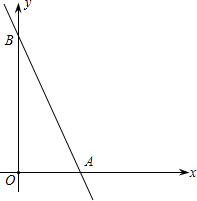 已知直线y=-2x+6交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B两点及x轴上另一点C,且AC=2.
已知直线y=-2x+6交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B两点及x轴上另一点C,且AC=2.查看答案和解析>>
科目:初中数学 来源: 题型:
 为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.
为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.| A、4.2 | B、4 |
| C、3.8 | D、3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 11 |
| 12 |
| 2 |
| 4 |
| 0.4 |
| 3 | 8 |
| π |
| 4 |
| • |
| 2 |
| • |
| 3 |
| 2 |
| 10 |
| 3 |
| 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com