【题目】如图，矩形ABCD中，AB=6，BC=4．
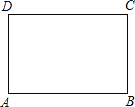
（1）画出以矩形的两条对称轴为坐标轴（x轴平行于AB）的平面直角坐标系，并写出点A，BC的中点E，DC的中点F的坐标；
（2）求过点A，E，F三点的抛物线的解析式，并写出此抛物线的顶点坐标．
【答案】（1）A（﹣3，﹣2），E（3，0），F（0，2）．
（2）抛物线y=﹣
x2+x+2，顶点（
）．
【解析】
试题分析：（1）根据矩形的对称性可知：E、F分别在x轴和y轴上，因此E（3，0），F（0，2）；由于DF=
CD=3，BE=BC=2，因此A（﹣3，﹣2）．
（2）可根据（1）题得出的A、E、F三点坐标，用待定系数法可求出抛物线的解析式．进而可用配方法或公式法求出抛物线顶点坐标．
解：（1）A（﹣3，﹣2），E（3，0），F（0，2）．
（2）易知：A（﹣3，﹣2）．
设抛物线的解析式为y=ax2+bx+c，由于抛物线过A、E、F三点，则有：
，
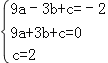解得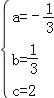
，
∴抛物线y=﹣x2+x+2，顶点（）．
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案科目：初中数学 来源： 题型：
【题目】生物学家发现一种病毒的长度约为0.00000403mm，数0.00000403用科学记数法表示为( )
A. 4.03×10﹣7 B. 4.03×10﹣6 C. 40.3×10﹣8 D. 430×10﹣9
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年我国西南五省市发生旱灾，尤其是西藏受灾最为严重，经济损失已经超过170亿，那么170亿用科学记数法表示为____________________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线经过三点A（1，0），B（4，0），C（0，﹣2）．
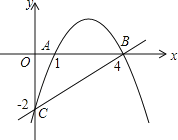
（1）求出抛物线的解析式；
（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以B，P，M为顶点的三角形与△OBC相似（相似比不为1）？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算(x﹣y+z)(x+y﹣z)的正确结果为( )
A. x2﹣y2+2xy﹣z2 B. x2﹣2xy+y2﹣z2
C. x2+2xy+y2﹣z2 D. x2+y2﹣2xy+z2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】每年4月23日是“世界读书日”，为了了解某校八年级500名学生对“世界读书日”的知晓情况，从中随机抽取了50名学生进行调查，在这次调查中，样本是（ ）
A. 500名学生 B. 所抽取的50名学生对“世界读书日”的知晓情况
C. 50名学生 D. 每一名学生对“世界读书日”的知晓情况
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边△ABC内有一点D，AD=5，BD=6，CD=4，将△ABD绕A点逆时针旋转，使AB与AC重合，点D旋转至点E，求∠CDE的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com