
【题目】计划拨款9万元从厂家购进50台电视机![]() 已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
![]() 若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
![]() 若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元
若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元![]() 在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
![]() 若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
【答案】(1)①甲、乙两种型号的电视机各购25台,②甲种型号的电视机购35台,丙种型号的电视机购15台;(2)为使销售时获利最多,应选择第![]() 种进货方案;(3)有四种进货方案:1、购进甲种电视27台,乙种电视20台,丙种电视3台,2、购进甲种电视29台,乙种电视15台,丙种电视6台,3、购进甲种电视31台,乙种电视10台,丙种电视9台,4、购进甲种电视33台,乙种电视5台,丙种电视12台.
种进货方案;(3)有四种进货方案:1、购进甲种电视27台,乙种电视20台,丙种电视3台,2、购进甲种电视29台,乙种电视15台,丙种电视6台,3、购进甲种电视31台,乙种电视10台,丙种电视9台,4、购进甲种电视33台,乙种电视5台,丙种电视12台.
【解析】(1)本题的等量关系是:两种电视的台数和=50台,买两种电视花去的费用=9万元.然后分进的两种电视是甲乙,乙丙,甲丙三种情况进行讨论.求出正确的方案;
(2)根据(1)得出的方案,分别计算出各方案的利润,然后判断出获利最多的方案;
(3)本题可先设两种电视的数量为未知数,然后根据三种电视的总量为50台,表示出另一种电视的数量,然后根据购进电视的费用总和为9万元,得出所设的两种电视的二元一次方程,然后根据自变量的取值范围,得出符合条件的方案.
![]() 设购进甲种x台,乙种y台.则有:
设购进甲种x台,乙种y台.则有:![]() ,解得
,解得![]() ;
;
设购进乙种a台,丙种b台.则有:![]() ,解得
,解得![]() ;
;![]() 不合题意,舍去此方案
不合题意,舍去此方案![]() .
.
设购进甲种c台,丙种e台.则有:![]() ,解得:
,解得:![]() .
.
通过列方程组解得有以下两种方案成立:
![]() 甲、乙两种型号的电视机各购25台.
甲、乙两种型号的电视机各购25台.
![]() 甲种型号的电视机购35台,丙种型号的电视机购15台;
甲种型号的电视机购35台,丙种型号的电视机购15台;
![]() 方案
方案![]() 获利为:
获利为:![]() 元
元![]() ;
;
方案![]() 获利为:
获利为:![]() 元
元![]() .
.
所以为使销售时获利最多,应选择第![]() 种进货方案;
种进货方案;
![]() 设购进甲种电视x台,乙种电视y台,则购进丙种电视的数量为:
设购进甲种电视x台,乙种电视y台,则购进丙种电视的数量为:![]() 台.
台.
![]() ,
,
化简整理,得![]() .
.
又因为![]() 、y、
、y、![]() ,且均为整数,
,且均为整数,
所以上述二元一次方程只有四组解:
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() .
.
因此,有四种进货方案:
1、购进甲种电视27台,乙种电视20台,丙种电视3台,
2、购进甲种电视29台,乙种电视15台,丙种电视6台,
3、购进甲种电视31台,乙种电视10台,丙种电视9台,
4、购进甲种电视33台,乙种电视5台,丙种电视12台.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)(﹣2)﹣1﹣|﹣ ![]() |+(3.14﹣π)0+4cos45°
|+(3.14﹣π)0+4cos45°
(2)已知x2﹣2x﹣7=0,求(x﹣2)2+(x+3)(x﹣3)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)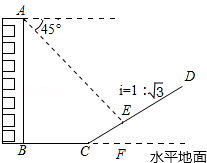
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=6,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C、D的对应点分别为C′、D′,折痕与边AD交于点F,当点B、C′、D′恰好在同一直线上时,AF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面积
(2) 在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标
(3) 是否存在一点P到AC、AB的距离相等,同时到点A、点B的距离也相等.若存在保留作图痕迹标出点P的位置,并简要说明理由;若不存在,请说明理由
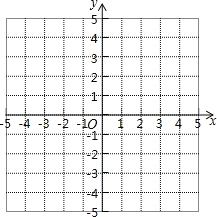
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题。
(1)计算:(﹣1)2015+( ![]() )﹣3﹣(π﹣3.1)0
)﹣3﹣(π﹣3.1)0
(2)计算:(﹣2x2y)23xy÷(﹣6x2y)
(3)先化简,再求值:[(2x+y)2+(2x+y)(y﹣2x)﹣6y]÷2y,其中x=-![]() ,y=3.
,y=3.
(4)用整式乘法公式计算: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,4)两点,与x轴交于另一点B,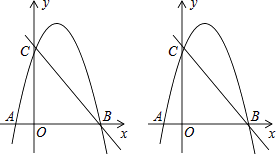
(1)求抛物线的解析式;
(2)求P在第一象限的抛物线上,P点的横坐标为t,过点P向x轴做垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式并求出m的最大值;
(3)在(2)的条件下,抛物线上一点D的纵坐标为m的最大值,连接BD,在抛物线是否存在点E(不与点A,B,C重合)使得∠DBE=45°?若不存在.请说明理由;若存在请求E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com