
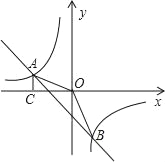
【题目】如图,一次函数y=kx﹣2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C.已知cos∠AOC=![]() ,OA=
,OA=![]() .
.
(1)求反比例函数及直线AB的解析式;
(2)求△AOB的面积.
【答案】(1)反比例函数的解析式为y=﹣![]() ,直线AB的解析式为y=﹣
,直线AB的解析式为y=﹣![]() x﹣2;(2)
x﹣2;(2)![]()
【解析】试题分析:(1)通过解直角三角形求出线段AC、OC的长度,从而得出点A的坐标,结合反比例函数图像上点的特点,可得出反比例函数解析式,由点A的坐标利用待定系数法即可求出直线AB的解析式;
(2)根据直线AB的解析式找出直线AB与x轴的交点坐标,再将一次函数解析式代入到反比例函数解析式中,解方程得出点B的坐标,分割三角形AOB,利用三角形的面积公式以及A、B的坐标即可得出结论.
试题解析:(1)∵AC⊥x轴,![]() ,
,
∴![]() ,
,
解得CO=2,
∴AC=![]() =1,
=1,
∴点A的坐标为(﹣2,1),
设反比例函数解析式为y=![]() ,则a=﹣2×1=﹣2,
,则a=﹣2×1=﹣2,
∴反比例函数的解析式为y=﹣![]() .
.
将点A(﹣2,1)代入到y=kx﹣1中,可得
1=﹣2k﹣2,
解得:k=﹣![]() ,
,
∴直线AB的解析式为y=﹣![]() x﹣2.
x﹣2.
(2)令一次函数y=﹣![]() x﹣2=0,
x﹣2=0,
解得:x=﹣![]() ,
,
即一次函数图象与x轴交于(﹣![]() ,0).
,0).
将y=﹣![]() x﹣2代入到反比例函数y=﹣
x﹣2代入到反比例函数y=﹣![]() 中,可得
中,可得
﹣![]() x﹣2=﹣
x﹣2=﹣![]() ,
,
即3x2+4x﹣4=0,
解得:x1=﹣2,x2=![]() .
.
∵y=﹣![]() x﹣2中,当x=
x﹣2中,当x=![]() 时,y=﹣3.
时,y=﹣3.
∴B(![]() ,﹣3).
,﹣3).
∴S△AOB=![]() ×
×![]() ×[1﹣(﹣3)]=
×[1﹣(﹣3)]=![]() .
.



科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)计算:6÷(-![]() +
+![]() ).
).

方方同学的计算过程如下:原式=6÷(-![]() )+6÷
)+6÷![]() =-12+18=6.
=-12+18=6.
请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程):
①999×(-15);②999×![]() +333×(-
+333×(-![]() )-999×
)-999×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
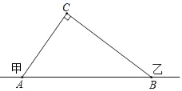
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蛋糕店为了吸引顾客,在A、B两种蛋糕中,轮流降低其中一种蛋糕价格,这样形成两种盈利模式,模式一:A种蛋糕利润每盒8元,B种蛋糕利润每盒15元;模式二:A种蛋糕利润每盒14元,B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒
(1)设按模式一销售A、B两种蛋糕所获利润为y1元,按模式二销售A、B两种蛋糕所获利润为y2元,分别求出y1、y2关于x的函数解析式;
(2)在同一个坐标系内分别画出(1)题中的两个函数的图象;

(3)若y始终表示y1、y2中较大的值,请问y是否为x的函数,并说说你的理由,并直接写出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)解方程组:
① 
②![]()
(2)计算
①(π-2013)0-(![]() )-2+|-4|;
)-2+|-4|;
②4(a+2)(a+1)-7(a+3)(a-3)
(3)因式分解
①a4-16
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
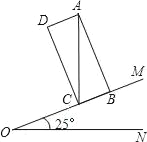
【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com