

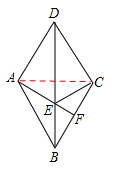
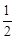 ∠BAC=30°。
∠BAC=30°。

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2。
ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2。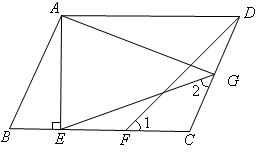
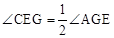 。
。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
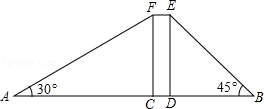
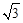 ≈1.73,
≈1.73,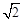 ≈1.41,
≈1.41, ≈2.24)
≈2.24)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0);查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
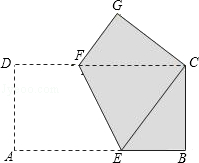
| A.16 | B. | C.22 | D.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com