
 如图,ABCD为一菱形铁皮,∠B=60°,边长AB=6,以A为圆心从中裁出一个面积最大的扇形,然后用所裁出的扇形围成一个圆锥的侧面,则该圆锥的高为( )
如图,ABCD为一菱形铁皮,∠B=60°,边长AB=6,以A为圆心从中裁出一个面积最大的扇形,然后用所裁出的扇形围成一个圆锥的侧面,则该圆锥的高为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 求出最大扇形的半径为3$\sqrt{3}$,求出扇形的弧长,再求出圆锥的半径,由勾股定理求出圆锥的高即可.
解答 解:连接AC,作AE⊥BC于E,如图所示: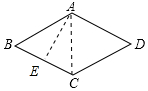
∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AE=AB•sin60°=3$\sqrt{3}$,
∴最大扇形的弧长=$\frac{120π×3\sqrt{3}}{180}$=2$\sqrt{3}$π,
∴圆锥的底面周长2πr=2$\sqrt{3}$π,
∴圆锥的底面半径r=$\sqrt{3}$,
由勾股定理得:圆锥的高=$\sqrt{(3\sqrt{3})^{2}-(\sqrt{3})^{2}}$=2$\sqrt{6}$;
故选:A.
点评 本题考查了菱形的性质、等边三角形的判定与性质、圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=9}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从装有22个红球、2个黄球的袋中摸出3个球,它们的颜色全不相同 | |
| B. | 通常温度降到0℃以下,纯净的水结冰 | |
| C. | 任意画一个三角形,其内角和是360° | |
| D. | 随意翻到一本书的某页,这页的页码是奇数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
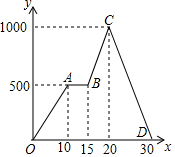 宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )
宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )| A. | 整个行进过程花了30分钟 | B. | 整个行进过程共走了1000米 | ||
| C. | 在图中停下来休息了5分钟 | D. | 返回时速度为100米/分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
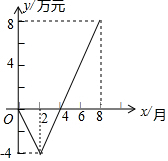 某超市今年年初因管理不善,效益较差,连续几个月出现亏损,后改革管理方法,实行股份制,员工积极性大增,业绩逐步上升,1-8月的累计利润y(万元)与时间x(月)之间的关系如图,根据图象回答:
某超市今年年初因管理不善,效益较差,连续几个月出现亏损,后改革管理方法,实行股份制,员工积极性大增,业绩逐步上升,1-8月的累计利润y(万元)与时间x(月)之间的关系如图,根据图象回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com