
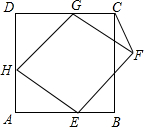
 ,DA上,AH=2,连接CF.
,DA上,AH=2,连接CF.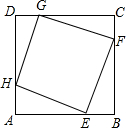 解:(1)∵正方形ABCD中,AH=2,
解:(1)∵正方形ABCD中,AH=2, ,即菱形EFGH的边长为2
,即菱形EFGH的边长为2 .
. ,
, ×4×2=4.
×4×2=4.
 ×2×(6-x)=6-x.
×2×(6-x)=6-x. ,
,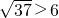 ,即点E已经不在边AB上.
,即点E已经不在边AB上. ,此时,当点E逐渐向右运动至点B时,HE的长(即菱形的边长)将逐渐变大,最大值为HE=2
,此时,当点E逐渐向右运动至点B时,HE的长(即菱形的边长)将逐渐变大,最大值为HE=2 .
. ,故0≤x≤2
,故0≤x≤2 .
. 时,S△FCG取得最小值为6-2
时,S△FCG取得最小值为6-2 .
. =1,所以,△FCG的面积不可能等于1.
=1,所以,△FCG的面积不可能等于1. .相应地,在△AHE中,AE=
.相应地,在△AHE中,AE=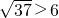 ,即点E已经不在边AB上.故不可能有S△FCG=1.
,即点E已经不在边AB上.故不可能有S△FCG=1.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
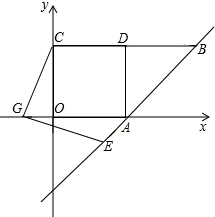
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 32 |
| x |
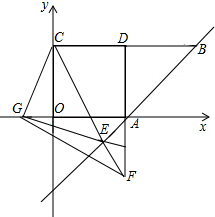
| OG+GF |
| DF |
查看答案和解析>>
科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:
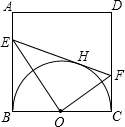 于E,交CD于F.
于E,交CD于F.| 13 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com