
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
【答案】(1)证明见解析;(2)BE+CF>EF.理由见解析.
【解析】试题分析:(1)先利用ASA判定△BGD≌△CFD,从而得出BG=CF;
(2)再利用全等的性质可得GD=FD,再有DE⊥GF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
试题解析:(1)∵BG∥AC,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
∵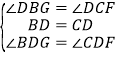
∴△BGD≌△CFD(ASA).
∴BG=CF.
(2)BE+CF>EF.
∵△BGD≌△CFD,
∴GD=FD,BG=CF.
又∵DE⊥FG,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2 , 请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,由若干个完全相同的棱长为 10 cm 的小正方体堆成一个几何体,如图 所示.
(1)这个几何体由多少个小正方体组成?请画出这个几何体的三视图.
(2)如果在这个几何体的表面(不包括底面)喷上黄色的漆,则在所有的小正方体中,有多少个只有一个面是黄色?有多少个只有两个面是黄色?有多少个只有三个面是黄色?
(3)假设现在你手里还有一些相同的小正方体,保持这个几何体的主视图、俯视图形状 不变,最多可以再添加几个小正方体?这时如果要重新给这个几何体表面(不包括底面) 喷上红色的漆,需要喷漆的面积比原几何体增加了还是减少了?增加或减少的面积是 多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
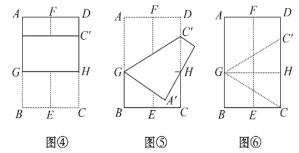
【题目】如图,将矩形纸片ABCD按如下顺序折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③),沿GH折叠,使点C落在DH上的C′处(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图⑥).
(1)求图②中∠BCB′=______度;
(2)图⑥中的△GCC′是_______三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司向甲、乙两所中学送水,每次送往甲中学7600升,乙中学4000升.已知人均送水量相同,甲中学师生人数是乙中学的2倍少20人.
(1)求这两所中学师生人数分别是多少;
(2)若送瓶装水,价格为1元/升;若用消防车送饮用水,不需购买,但需配送水塔,容量500升的水塔售价为520元/个,其他费用不计.请问这次乙中学用瓶装水花费少还是饮用消防车送水花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
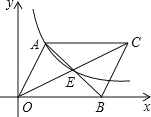
【题目】如图,平行四边形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点, 若平行四边形AOBC的面积为30,则k=__________.
(k>0)经过A、E两点, 若平行四边形AOBC的面积为30,则k=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com