
| 苹果品种 | A | B | C |
| 每辆汽车(吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利(百元) | 6 | 8 | 5 |
分析 (1)根据有20辆汽车装运A、B、C三种水果,可以表示出有20-x-y辆车装运C种水果,从而得出答案,
(2)从而根据水果总吨数为42,再根据(1)中运费与车辆数即可表示出w,最后由一次函数的性质即可求最大利润以及此时相应的车辆调配方案.
解答 解:(1)由题意得:
2.2x+2.1y+2(20-x-y)=42,
化简得:y=20-2x,
∵$\left\{\begin{array}{l}{x≥2}\\{20-2x≥2}\end{array}\right.$,
∴x的取值范围是:2≤x≤9.
(2)由题意得:
W=6×2.2x+8×2.1(-2x+20)+5×2(20-x-y),
=-10.4x+336,
∵k=-10.4<0,且2≤x≤9,
∴当x=2时,W有最大值,
w最大=-10.4×2+336=315.2(百元),
∴A:2辆;B:16辆;C:2辆.
∴相应的车辆分配方案为:
2辆车装运A种水果,用16辆车装运B种水果,有20-x-y=2辆车装运C种水果.
点评 此题主要考查了一次函数的应用,得出y与x的关系式,以及利用一次函数增减性求最值是解决问题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
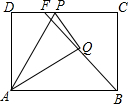 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )| A. | 3 | B. | 2 | C. | 4-$\sqrt{7}$ | D. | 4-$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{600}{x+50}$=$\frac{400}{x}$ | B. | $\frac{600}{x}$=$\frac{400}{x-50}$ | C. | $\frac{600}{x-50}$=$\frac{400}{x}$ | D. | $\frac{600}{x}$=$\frac{400}{x+50}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
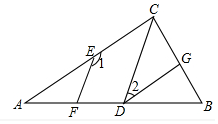 已知:如图,EF∥CD,∠1+∠2=180°.
已知:如图,EF∥CD,∠1+∠2=180°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.076×108 | B. | 2076×106 | C. | 0.2076×108 | D. | 2.076×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com