
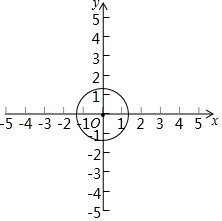 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.分析 (1)由梦之点的定义可求得P点坐标,再利用待定系数法可求得反比例函数解析式;
(2)①设⊙O上的梦之点坐标为(a,a),由圆的半径,根据勾股定理可得到关于a的方程,可求得a的值,则可得梦之点的坐标;
②分两种情况进行讨论:当MN为y=-x+b时,m=b-3,当直线MN平移至与⊙O相切时,且切点在第三象限时,b取得最小值,当直线MN平移至与⊙O相切时,且切点在第一象限时,b取得最大值,据此可得m的取值范围为-5≤m≤-1;当直线MN为y=x+b时,同理可得,m的取值范围为1≤m≤5.
解答 解:(1)∵P(2,b)是梦之点,
∴b=2,
∴P(2,2),
将P(2,2)代入y=$\frac{n}{x}$中,得n=4,
∴反比例函数解析式是y=$\frac{4}{x}$;
(2)①∵⊙O的半径是$\sqrt{2}$,
设⊙O上梦之点坐标是(a,a),
∴a2+a2=($\sqrt{2}$)2,
∴a2=1,
a=1或a=-1,
∴⊙O上所有梦之点坐标是(1,1)或(-1,-1);
②由(1)知,异于点P的梦之点是(-2,-2),
∵tan∠OAQ=1,
∴∠OAQ═45°,
∵MN∥l或MN⊥l,
∴直线MN为y=-x+b或y=x+b,
当MN为y=-x+b时,m=b-3,
由图可知,当直线MN平移至与⊙O相切时,且切点在第三象限时,b取得最小值,
此时MN记为M1N1,其中N1为切点,T1为直线与y轴的交点.
∵△OT1N1为等要直角三角形,
∴ON1=$\sqrt{2}$,
∴OT1=2,
∴b的最小值是-2,
∴m的最小值是-5,
当直线MN平移至与⊙O相切时,且切点在第一象限时,b取得最大值,
此时MN记为M2N2,
其中 N2为切点,T2为直线M2N2与y轴的交点.
同理可得,b的最大值为2,m的最大值为-1.
∴m的取值范围为-5≤m≤-1;
当直线MN为y=x+b时,同理可得,m的取值范围为1≤m≤5,
综上所述,m的取值范围为-5≤m≤-1或1≤m≤5.
点评 本题属于反比例函数综合题,主要考查了反比例函数的图象与性质,等腰直角三角形的性质,切线的性质,待定系数法求反比例函数解析式的综合应用,解决问题的关键是依据根据MN∥l或MN⊥l,可得直线MN为y=-x+b或y=x+b,画出图形进行分析,解题时注意分类思想的运用.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
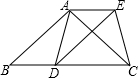 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
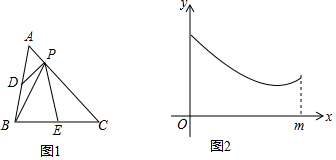
| A. | PD | B. | PB | C. | PE | D. | PC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运行区间 | 公布票价 | 学生票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 三等座 |
| 无锡 | 上海 | 81(元) | 68(元) | 51(元) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
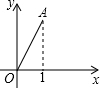 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )| A. | (0,2) | B. | (0,-2) | C. | (-1,-$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
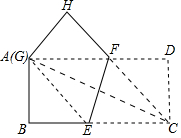 将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.
将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com