
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买![]() 、
、![]() 两种型号的污水处理设备共10台,用于同时治理不同成分的污水,若购买
两种型号的污水处理设备共10台,用于同时治理不同成分的污水,若购买![]() 型6台,
型6台,![]() 型4台需112万,购买
型4台需112万,购买![]() 型4台,
型4台,![]() 型6台则需108万元.
型6台则需108万元.
(1)求出![]() 型、
型、![]() 型污水处理设备的单价;
型污水处理设备的单价;
(2)经了解,一台![]() 型设备每月可处理污水220吨,一台
型设备每月可处理污水220吨,一台![]() 型设备每月可处理污水190吨,如果该企业计划用不超过106万元的资金购买这两种设备,而且使这两种设备每月的污水处理量不低于2005吨,请通过计算说明这种方案是否可行.
型设备每月可处理污水190吨,如果该企业计划用不超过106万元的资金购买这两种设备,而且使这两种设备每月的污水处理量不低于2005吨,请通过计算说明这种方案是否可行.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
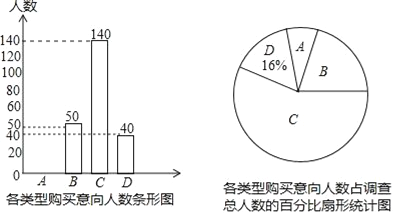
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何探究题
(1)发现:在平面内,若BC=a,AC=b,其中a>b.
当点A在线段BC上时(如图1),线段AB的长取得最小值,最小值为 ;
当点A在线段BC延长线上时(如图2),线段AB的长取得最大值,最大值为 .
(2)应用:点A为线段BC外一动点,如图3,分别以AB、AC为边,作等边△ABD和等边△ACE,连接CD、BE.
①证明:CD=BE;
②若BC=3,AC=1,则线段CD长度的最大值为 .
(3)拓展:如图4,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个六边形的花坛被分割成7个部分,其中四边形PRBA,RQDC,QPFE为正方形。记正方形PRBA,RQDC,QPFE的面积分别为![]() ,
,![]() ,
,![]() , RH⊥PQ,垂足为H。
, RH⊥PQ,垂足为H。
(1)若PR⊥QR,![]() =16,
=16,![]() =9,则
=9,则![]() = ,RH= ;
= ,RH= ;
(2)若四边形PRBA,RQDC,QPFE的面积分别为25m2、13m2、36m2

①求△PRQ的面积;
②请判断△PRQ和△DEQ的面积的数量关系,并证明你的结论;
③六边形花坛ABCDEF的面积是 m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC.
(1)判断射线EF与BD的位置关系,并说明理由;
(2)求∠C,∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() . (第一步)
. (第一步)
去括号,得 ![]() . (第二步)
. (第二步)
移项,合并同类项,得 ![]() . (第三步)
. (第三步)
解得 ![]() . (第四步)
. (第四步)
经检验,![]() 是原方程的解. (第五步)
是原方程的解. (第五步)
(1)小明解答过程是从第 步开始出错的,原方程化为第一步的根据是 .
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
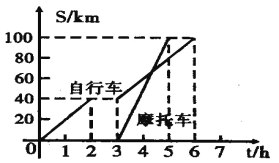
【题目】已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,下图反映的是这两个人行驶过程中路程s(km)和时间t(h)的关系,请根据图象回答下列问题:
(1)甲地与乙地相距 千米.
(2)摩托车比自行车晚出发 小时.
(3)求摩托车行驶的路程s与时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com