
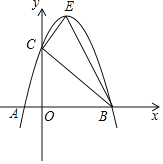
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,点C为抛物线与y轴的交点.
,点C为抛物线与y轴的交点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点E为直线BC上方抛物线上的一点,请求出
若点E为直线BC上方抛物线上的一点,请求出![]() 面积的最大值.
面积的最大值.
![]() 在
在![]() 条件下,是否存在这样的点
条件下,是否存在这样的点![]() ,使得
,使得![]() 为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.
为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.
【答案】(1)![]() .(2)当
.(2)当![]() 时,
时,![]() 面积取最大值,最大值为
面积取最大值,最大值为![]() .(3)点D的坐标为
.(3)点D的坐标为![]() 、
、![]() 、
、![]() 、
、![]() 或
或![]()
【解析】分析:![]() 根据点A、B的坐标利用待定系数法即可求出抛物线的解析式;
根据点A、B的坐标利用待定系数法即可求出抛物线的解析式;
![]() 过点E作
过点E作![]() 轴,交BC于点F,利用二次函数图象上点的坐标特征可找出点C的坐标,根据点B、C的坐标利用待定系数法即可求出直线BC的解析式,设点E的坐标为
轴,交BC于点F,利用二次函数图象上点的坐标特征可找出点C的坐标,根据点B、C的坐标利用待定系数法即可求出直线BC的解析式,设点E的坐标为![]() ,则点F的坐标为
,则点F的坐标为![]() ,进而可得出EF的长度,利用三角形的面积公式可得出
,进而可得出EF的长度,利用三角形的面积公式可得出![]() ,配方后利用二次函数的性质即可求出
,配方后利用二次函数的性质即可求出![]() 面积的最大值;
面积的最大值;
![]() 分
分![]() 、
、![]() 、
、![]() 三种情况考虑,根据等腰三角形的性质结合两点间的距离公式,即可得出关于m的一元二次
三种情况考虑,根据等腰三角形的性质结合两点间的距离公式,即可得出关于m的一元二次![]() 或一元一次
或一元一次![]() 方程,解之即可得出结论.
方程,解之即可得出结论.
详解:![]() 将
将![]() 、
、![]() 代入
代入![]() ,
,
得:![]() ,解得:
,解得:![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
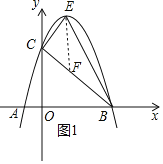
![]() 过点E作
过点E作![]() 轴,交BC于点F,如图1所示.
轴,交BC于点F,如图1所示.
当![]() 时,
时,![]() ,
,
![]() 点C的坐标为
点C的坐标为![]() .
.
设直线BC的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,得:
,得:
![]() ,解得:
,解得:![]() ,
,
![]() 直线BC的解析式为
直线BC的解析式为![]() .
.
设点E的坐标为![]() ,则点F的坐标为
,则点F的坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 面积取最大值,最大值为
面积取最大值,最大值为![]() .
.
![]() 由
由![]() 可知点E的坐标为
可知点E的坐标为![]()
![]() 为等腰三角形分三种情况
为等腰三角形分三种情况![]() 如图
如图![]() :
:

![]() 当
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点D的坐标为
点D的坐标为![]() 或
或![]() ;
;
![]() 当
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,
![]() 点D的坐标为
点D的坐标为![]() ;
;
![]() 当
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点D的坐标为
点D的坐标为![]() 或
或![]()
综上所述:当点D的坐标为![]() 、
、![]() 、
、![]() 、
、![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】观察下列等式:
①sin30°=![]() ,cos60°=
,cos60°=![]() ;
;
②sin45°=![]() ,cos45°=
,cos45°=![]() ;
;
③sin60°=![]() ,cos30°=
,cos30°=![]() .
.
(1)根据上述规律,计算sin2α+sin2(90°-α)= .
(2)计算:sin21°+sin22°+sin23°+…+sin289°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在四等分的转盘上依次标有“0元”、“10元”、“30元”、“50元”字样,购物每满300元可以转动转盘2次,每次转盘停下后,顾客可以获得指针所指区域相应金额的购物券![]() 指针落在分界线上不计次数,可重新转动一次
指针落在分界线上不计次数,可重新转动一次![]() ,一个顾客刚好消费300元,并参加促销活动,转了2次转盘.
,一个顾客刚好消费300元,并参加促销活动,转了2次转盘.
![]() 求出该顾客可能落得购物券的最高金额和最低金额;
求出该顾客可能落得购物券的最高金额和最低金额;
![]() 请用列表法或画树状图法求出该顾客获购物金额不低于50元的概率.
请用列表法或画树状图法求出该顾客获购物金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材母题 点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.
(1)用含有x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积为多少?
(3)△OPA的面积能大于24吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
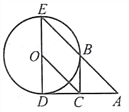
【题目】如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于点B,且四边形BCOE是平行四边形。
(1)BC是⊙O的切线吗?若是,给出证明:若不是,请说明理由;
(2)若⊙O半径为1,求AD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com