
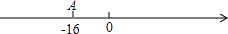 已知A、B两地相距50米,小乌龟从A地出发前往B地,第一次它前进1米,第二次它后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为-16.
已知A、B两地相距50米,小乌龟从A地出发前往B地,第一次它前进1米,第二次它后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为-16.分析 (1)在数轴上表示-16的点移动50个单位后,所得的点表示为-16-50=-66或-16+50=34;
(2)数轴上点的移动规律是“左减右加”.依据规律计算即可;
(3)根据100为偶数可得在数轴上表示的数,再根据两点间的距离公式即可求解.
解答 解:(1)-16+50=34,-16-50=-66.
答:B地在数轴上表示的数是34或-66.
(2)第七次行进后:1-2+3-4+5-6+7=4,
第八次行进后:1-2+3-4+5-6+7-8=-4,
因为点P、Q与A点的距离都是4米,
所以点P、点Q到A地的距离相等;
(3)当n为100时,它在数轴上表示的数为:
-16+1-2+3-4+…+(100-1)-100=$\frac{-32-100}{2}$=-66,
34-(-66)=100(米).
答:小乌龟到达的点与点B之间的距离是100米.
点评 本题考查了数轴,解题的关键是明确题意,发现题目中的规律,找出所求问题需要的条件.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | {x|a<x<$\frac{1}{a}$} | B. | {x|$\frac{1}{a}$<x<a} | C. | {x|x<a或x>$\frac{1}{a}$} | D. | {x|x<$\frac{1}{a}$或x>a} |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a+b)(2a-b) | B. | (-2a+b)(b-2a) | C. | (-2a+b)(-2a-b) | D. | (2a-b)-(2a-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,AC=BC,BD⊥BC于B,点E在 BC上,CE=BD,DC、AE交于点F.试问DC与AE有何关系,请说明理由.
如图,△ABC中,∠ACB=90°,AC=BC,BD⊥BC于B,点E在 BC上,CE=BD,DC、AE交于点F.试问DC与AE有何关系,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
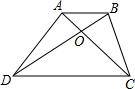 如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知Rt△ABC,∠ACB=90°,AD平分∠BAC与BC交于D点,M、N分别在线段AD、AC上的动点,连接MN、MC,当MN+MC最小时,画出M、N的位置.已知△ABC的面积为12cm2,AB=6cm,求MN+MC的最小值.
如图,已知Rt△ABC,∠ACB=90°,AD平分∠BAC与BC交于D点,M、N分别在线段AD、AC上的动点,连接MN、MC,当MN+MC最小时,画出M、N的位置.已知△ABC的面积为12cm2,AB=6cm,求MN+MC的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com